|
|
|
|
|
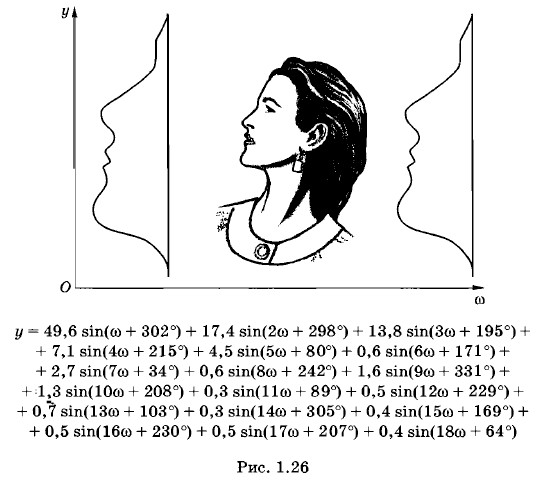
Глава 1. Механические колебания Сложение гармонических колебаний. Спектр колебанийСложение гармонических колебаний различных частотГораздо более сложная картина возникает при сложении колебаний различных частот. Мы этот случай подробно рассматривать не будем. Ограничимся лишь несколькими замечаниями. При сложении гармонических колебаний различных частот результирующее колебание уже не будет гармоническим. Если складываются колебания с кратными частотами, то результирующее колебание оказывается периодическим, а его форма может очень сильно отличаться от синусоиды. На рисунке 1.26 представлен результат сложения 18 гармонических синусоидальных колебаний с различными амплитудами, начальными фазами и различными, но кратными частотами. Получился профиль девушки, фотография которой помещена рядом. Такую форму будет иметь график зависимости смещения колеблющейся точки от времени (временна́я развертка колебаний). Каждый, если не пожалеет времени, может убедиться, что вас не пытаются ввести в заблуждение. Кстати, можно убедиться и в том, что профиль девушки будет с течением времени периодически повторяться.
Спектр колебанийМожно поставить обратную задачу: заданы периодические, но не гармонические колебания координаты, внешней силы или какой-либо другой физической величины. Надо представить данное сложное колебание в виде суммы гармонических колебаний. Развиты строгие математические методы, которые позволяют это сделать для любого сколь угодно сложного колебания. Например, по заданному графику, изображающему профиль девушки (см. рис. 1.26), можно найти амплитуды, частоты и фазы гармонических функций, сумма которых дает исходное колебание. Мы не будем касаться этой сложной математической задачи. Обратим внимание лишь на одно наиболее существенное обстоятельство. Важным является определение частот тех гармонических колебаний, на которые разлагается сложное колебание. Совокупность частот сложного колебания называется его частотным спектром или просто спектром. Колебания каждой частоты представлены с той или иной амплитудой. Значение анализа спектрального состава сложного колебания связано с резонансом. Допустим, на колебательную систему с собственной частотой колебаний ω0 действует внешняя сложная периодическая сила. Тогда наша колебательная система будет заметно отзываться только на гармоническую составляющую сложного колебания, частота которой совпадает с собственной частотой колебательной системы или близка к ней. При малых силах трения в системе резонансная кривая имеет резкий максимум и гармонические составляющие периодической силы с частотами, заметно отличающимися от резонансной, не вызовут «отклика» системы. Если в спектре внешней силы нет частот, близких к собственной частоте колебаний системы, то амплитуда вынужденных колебаний системы будет мала. Благодаря этому с помощью набора колебательных систем с различными собственными частотами можно экспериментально определить спектр колебаний внешней силы. Например, частотомер, о котором говорилось в § 1.10, позволяет установить спектр сложных электрических колебаний силы тока. Для этого обмотку электромагнита нужно питать этим током. В такт с колебаниями силы тока будет колебаться планка с пластинами. Лишь те пластины, собственные частоты колебаний которых присутствуют в спектре колебаний тока, будут иметь заметную амплитуду колебаний. Непериодическую функцию времени тоже можно представить в виде бесконечной суммы гармонических колебаний. Но частоты этих колебаний могут быть любыми.
|
|
|