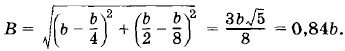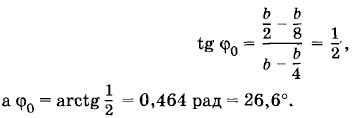|
|
|
|
|
Глава 1. Механические колебания § 1.13. Примеры решения задач на тему: Механические колебанияЗадача 3
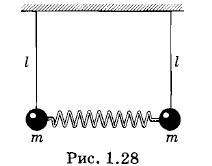
Два математических маятника, длиной l каждый, связаны невесомой пружиной (рис. 1.28). Жесткость пружины равна k. При равновесии маятники занимают вертикальное положение, и пружина недеформирована. Определите частоты малых колебаний двух связанных маятников в случаях, когда маятники отклонены в одной плоскости на равные углы в одну сторону (колебания в фазе) и в противоположные стороны (колебания в противофазе). Решение. Отклоним оба маятника от вертикали в одну и ту же сторону на одинаковый угол. Пружина при таком отклонении не будет деформирована. Легко сообразить, что отпущенные из этого положения маятники будут колебаться в фазе с частотой При отклонении в разные стороны на одинаковые углы колебания маятников будут происходить в противофазе, и пружина будет деформироваться. Для того чтобы подсчитать частоту этих колебаний, найдем силу, возвращающую маятники в положение равновесия. При отклонении на угол φ модуль силы, действующей со стороны пружины на тело массой m, согласно закону Гука равен Fy = k'Δl. Но жесткость половины пружины k' = 2k, а растяжение этой половины Δl = l sin φ. Следовательно, Fy = 2kl sin φ.
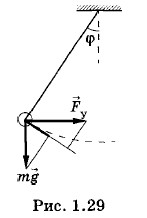
Сумма проекций силы тяжести и силы упругости на касательную к окружности (обозначим ее через F) равна: F = mg sin φ + 2kl sin φ cos φ (рис. 1.29). Так как при малых углах cos &phi ≈ 1, то
Для математического маятника эта проекция равна mg sin φ. При этом частота колебаний при малых углах φ определяется формулой
Задача 4Два неподвижных точечных заряда +q0 расположены в точках B и С на расстоянии r друг от друга. Вдоль оси симметрии системы этих зарядов может перемещаться шарик массой m, несущий точечный заряд —q (рис. 1.30). Считая смещение отрицательного заряда от прямой ВС, соединяющей положительные заряды, малым по сравнению с r, определите период Т колебаний отрицательного заряда.
Решение. Направим ось X вдоль оси симметрии системы данных зарядов (рис. 1.31), а начало координат совместим с серединой отрезка ВС. Сместим заряд -q на небольшое расстояние ОА = х от положения равновесия О. Тогда на заряд —q со стороны зарядов +q0 начнут действовать силы Fх = -2F1 sin α. (1.13.9) Так как угол а мал, то Модуль силы
Смещение х — малая величина, а х2 — величина второго порядка малости и ею можно пренебречь. Следовательно,
Заменив в выражении (1.13.9) F1 и sin α их значениями, получим:
Согласно второму закону Ньютона
Уравнение (1.13.11) описывает гармонические колебания, совершающиеся с циклической частотой
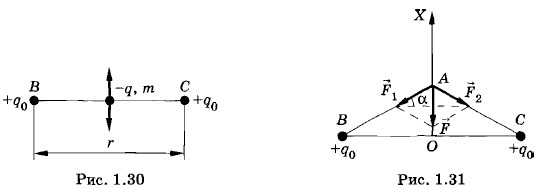
Отсюда период колебаний отрицательного заряда будет равен:
Задача 5Сложите гармонические колебания:
Определите амплитуду В и начальную фазу φ0 результирующего колебания.
Решение. Приведем данные в условии задачи уравнения к виду
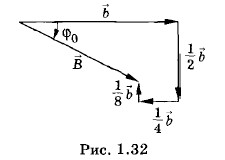
и построим векторную диаграмму (рис. 1.32). На векторной диаграмме модуль вектора
Из этой же векторной диаграммы находим, что
|
|
|



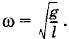
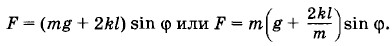
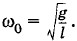 В нашем случае роль g играет величина
В нашем случае роль g играет величина 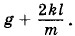 Следовательно,
Следовательно,
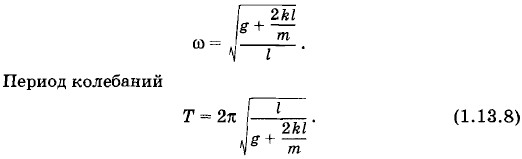
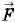 1 и
1 и 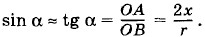
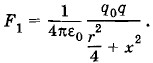
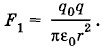

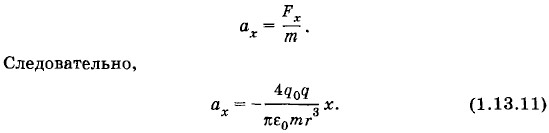
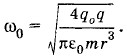
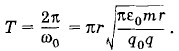
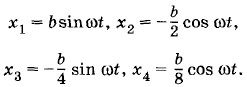
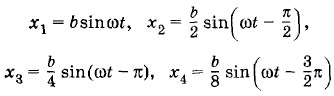
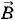 — амплитуда результирующего колебания. Она равна
— амплитуда результирующего колебания. Она равна