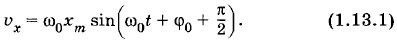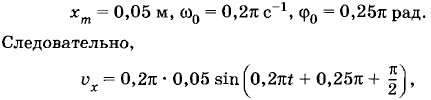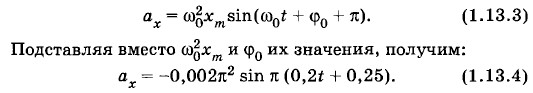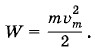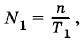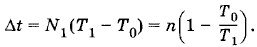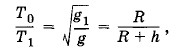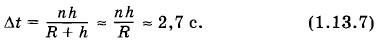Примеры решения задач на тему: Механические колебания

При решении задач на колебательное движение следует использовать кинематические выражения для описания гармонических колебаний: формулы для координаты (1.4.3) и (1.4.4), скорости (1.7.1) и ускорения (1.7.2).

Надо хорошо себе представлять динамику колебаний груза на пружине и математического маятника, знать дифференциальное уравнение гармонических колебаний (1.2.6), уметь составлять уравнения движения, описывающие колебания в простых системах.

Надо также знать формулы для периодов колебаний груза на пружине и математического маятника (1.5.4) и (1.5.6). Следует понимать элементарную теорию вынужденных колебаний, знать формулу для амплитуды этих колебаний при резонансе (1.10.2). Наконец, надо уметь в простейших случаях складывать гармонические колебания.

Задача 1

Материальная точка массой 50 г колеблется по закону х = 0,05 sin π (0,2t + 0,25)*. Напишите уравнения для скорости и ускорения этой точки. Найдите максимальную силу, действующую на точку, и полную энергию колеблющейся точки.

* Здесь и в дальнейшем в уравнениях для гармонических колебаний все данные выражены в единицах СИ.

Решение. Согласно формуле (1.7.1) уравнение для скорости точки имеет вид:

Из данного в условии задачи уравнения для координаты имеем:

или

υ_x = 0,01π sin π (0,2t + 0,75). (1.13.2)

Уравнение для ускорения гармонически колеблющейся точки согласно формуле (1.7.2) выглядит так:

Максимальная сила, действующая на точку, согласно второму закону Ньютона равна:

F_m = mа_m.

Из выражения (1.13.4) видно, что а_m = 0,002π² м/с² ≈ 0,02 м/с². Следовательно,

F_m = 1 • 10^-3 Н.

Полная энергия колеблющейся точки согласно формуле (1.7.6) равна:

Из уравнения (1.13.2) находим, что υ_m = 0,01π м/с, поэтому

W ≈ 2,5 • 10^-6 Дж.

Задача 2

Часы, период колебаний маятника которых Т₀ = 1 с, на поверхности Земли идут точно. На сколько будут отставать эти часы за сутки, если их поднять на высоту h — 200 м над поверхностью Земли?

Решение. На поверхности Земли период колебаний маятника равен:

На высоте h над Землей период колебаний маятника составит

где g₁ — ускорение свободного падения на этой высоте. Число колебаний маятника за сутки на высоте h равно:

где n = 24 • 3600 с.

Следовательно, на высоте h над Землей часы отстанут за сутки на время

Из выражений (1.13.5) и (1.13.6) находим, что отношение периодов равно:

где R = 6400 км — радиус Земли.

Следовательно,

Окончание параграфа >>>