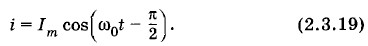|
|
|
|
|
Глава 2. Электрические колебания Формула ТомсонаСтрогий вывод формулы ТомсонаРешение уравнения (2.3.11) в общем случае, т. е. нахождение зависимости заряда и силы тока от времени, слишком сложно. Мы ограничимся случаем, когда резистор в контуре отсутствует и членом iR = -q'R можно пренебречь. Тогда уравнение (2.3.11) упрощается и его можно записать в виде
Теперь, наконец, вы в полной мере сможете оценить те усилия, которые были затрачены для изучения колебаний груза на пружине и математического маятника. Ведь уравнение (2.3.12) ничем, кроме обозначений, не отличается от уравнения (1.2.4), описывающего колебания груза на пружине. При замене m → L, ах = х" → q", Но уравнение (1.2.4) или эквивалентное ему уравнение (1.4.1) нами уже решено. Поэтому, зная, как колеблется груз, мы сразу можем сказать, как происходят колебания в контуре. Разделив правую и левую части уравнения (2.3.12) на! и введя обозначение
А это то же самое, что и уравнение (1.4.1). В уравнении (1.4.1) ω0 — циклическая частота колебаний. Значит, и величина ω0, определяемая выражением (2.3.13), тоже является частотой колебаний, но теперь уже частотой электрических колебаний (заряда, силы тока и других величин). Период свободных колебаний в контуре равен:
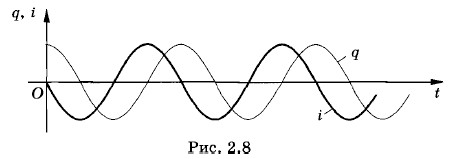
Это и есть формула Томсона. Конечно, и без каких-либо уравнений мы могли бы сообразить, что период Т должен увеличиваться с ростом индуктивности L и емкости С. Действительно, при увеличении L сила тока медленнее нарастает со временем и медленнее падает до нуля. А чем больше емкость, тем большее время требуется для перезарядки конденсатора. Но получить формулу (2.3.15) строго без уравнения (2.3.14) мы бы не смогли. Гармонические колебания заряда и силы токаПодобно тому, как координата при механических колебаниях меняется по гармоническому закону, точно также заряд конденсатора меняется по закону синуса или косинуса: q = qm sin (ω0t + φ0) или q = qm cos (ω0t + φ0). (2.3.16) Здесь qm — амплитуда колебаний заряда, а φ0 — начальная фаза колебаний. Эти величины определяются начальными условиями, т. е. значениями заряда и силы тока в начальный момент времени: q(0) = q0 и i(0) = i0. Если в начальный момент времени g(0) = q0, а i(0) = 0, то колебания совершаются по косинусоидальному закону с нулевой начальной фазой* и амплитудой qm = q0: q = q0 cos ω0t. (2.3.17) * Именно такой случай описан в § 2.2, когда колебания в контуре начинались после замыкания цепи предварительно заряженного конденсатора. Точно так же изменяется координата груза на пружине, если вы вывели груз из положения равновесия и не сообщили ему начальной скорости. Сила тока также совершает гармонические колебания. Если q = qm cos (ω0t + φ0), то
где Im = ω0qm — амплитуда колебаний силы тока. Колебания силы тока смещены по фазе относительно колебаний заряда на
Колебания заряда и силы тока для этого случая графически представлены на рисунке 2.8.
В действительности из-за энергетических потерь колебания будут затухающими. Чем больше сопротивление R, тем больше будет период колебаний. При достаточно большом сопротивлении колебания не возникают. Конденсатор разрядится, но перезарядки не произойдет.
|
|
|




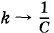 и х → q мы в точности получим уравнение (2.3.12) вместо (1.2.4).
и х → q мы в точности получим уравнение (2.3.12) вместо (1.2.4).
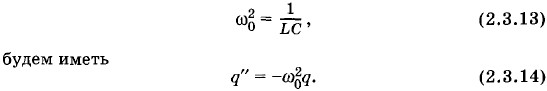
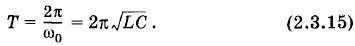
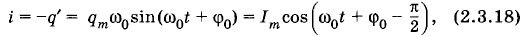
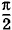 . При начальных условиях q(0) = q0, i(0) = 0
. При начальных условиях q(0) = q0, i(0) = 0