|
|
|
|
|
Глава 2. Электрические колебания § 2.10. Мощность в цепи переменного токаМощность в цепи постоянного тока определяется произведением напряжения на силу тока: Р = UI. (2.10.1) Физический смысл этой формулы прост: так как напряжение U численно равно работе электрического поля по перемещению единичного заряда, то произведение UI характеризует работу по перемещению заряда за единицу времени, протекающего через поперечное сечение проводника, т. е. является мощностью. Мощность электрического тока на данном участке цепи положительна, если энергия поступает к этому участку из остальной сети, и отрицательна, если энергия с этого участка возвращается в сеть. На протяжении очень малого интервала времени квазистационарный переменный ток можно считать неизменным. Поэтому мгновенная мощность в цепи переменного тока определяется такой же формулой: р = ui. (2.10.2) Если напряжение на концах цепи меняется по гармоническому закону u = Um cos ωt*, * С тем же успехом, разумеется, вместо u = Um cos ωt можно было бы записать u = Um sin ωt. то и сила тока будет меняться со временем гармонически с той же частотой, но в общем случае будет сдвинута по фазе относительно напряжения: i = Im cos (ωt + φc), где φc — сдвиг фаз между силой тока и напряжением. Поэтому для мгновенной мощности можно записать: p = ui = UmIm cos ωt cos (ωt + φc). (2.10.3) При этом мощность меняется со временем как по модулю, так и по знаку. В течение одной части периода энергия поступает к данному участку цепи (р > 0), но в течение другой части периода некоторая доля энергии вновь возвращается в сеть (р < 0). Как правило, во всех случаях нам надо знать среднюю мощность на участке цепи за достаточно большой промежуток времени, включающий много периодов. Для этого достаточно определить среднюю мощность за один период. Чтобы найти среднюю мощность за период, преобразуем сначала формулу (2.10.3) таким образом, чтобы выделить в ней член, не зависящий от времени. С этой целью воспользуемся известной формулой для произведения двух косинусов:
В рассматриваемом случае α = ωt и β = ωt + φc. Поэтому
Но среднее значение второго члена за период равно нулю (см. § 2.5). Следовательно, средняя мощность за период равна первому члену, не зависящему от времени:
Переходя к действующим значениям силы тока и напряжения, получим:
Эту величину называют просто мощностью переменного тока на участке цепи и обозначают через Р:
Таким образом, мощность переменного тока на участке цепи определяется именно действующими значениями силы тока и напряжения. Она зависит также от сдвига фаз φc между напряжением и током. Множитель cos φc в формуле (2.10.4) называется коэффициентом мощности. В случае, когда
Лишь при наличии проводника с активным сопротивлением в цепи, не содержащей движущихся проводников, электромагнитная энергия превращается во внутреннюю энергию проводника, который нагревается. Обратного превращения внутренней энергии в электромагнитную на участке с активным сопротивлением уже не происходит. Для цепи, изображенной на рисунке 2.20, UR = IR = U cos φc. Подставив в формулу (2.10.4) вместо U cos φc произведение силы тока I на R, получим следующее выражение для мощности: P = I2R. (2.10.5) Оно аналогично закону Джоуля—Ленца для постоянного тока. Формула (2.10.5) подтверждает сказанное выше о роли активного сопротивления. Но надо иметь в виду, что формула (2.10.4) справедлива всегда, а формула (2.10.5) выполняется лишь для частного случая. При проектировании цепей переменного тока нужно добиваться, чтобы cos φc не был мал. Иначе значительная часть энергии будет циркулировать по проводам от генератора к потребителям и обратно. Так как провода обладают активным сопротивлением, то при этом энергия расходуется на нагревание проводов. Неблагоприятные условия для потребления энергии возникают при включении в сеть электродвигателей, так как их обмотка имеет малое активное сопротивление и большую индуктивность. Для увеличения cos φc в сетях питания предприятий с большим числом электродвигателей включают специальные компенсирующие конденсаторы. Нужно также следить, чтобы электродвигатели не работали вхолостую или с недогрузкой. Это уменьшает коэффициент мощности всей цепи. Повышение cos φc является важной народнохозяйственной задачей, так как позволяет с максимальной отдачей использовать генераторы электростанций и снизить потери энергии. Это достигается правильным проектированием электрических цепей. Запрещается использовать устройства с cos φc < 0,85.
|
|
|



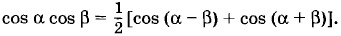
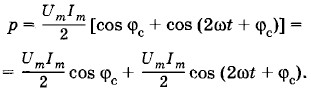
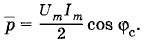
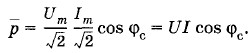

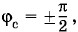 энергия, поступающая к участку цепи за период, равна нулю, хотя в цепи и существует ток. Так будет, в частности, если цепь содержит только катушку индуктивности или только конденсатор.
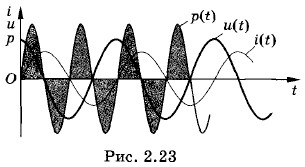
Как же средняя мощность может оказаться равной нулю при наличии тока в цепи? Это поясняют приведенные на рисунке 2.23 графики изменения со временем мгновенных значений напряжения, силы тока и мощности при
энергия, поступающая к участку цепи за период, равна нулю, хотя в цепи и существует ток. Так будет, в частности, если цепь содержит только катушку индуктивности или только конденсатор.
Как же средняя мощность может оказаться равной нулю при наличии тока в цепи? Это поясняют приведенные на рисунке 2.23 графики изменения со временем мгновенных значений напряжения, силы тока и мощности при  (чисто индуктивное сопротивление участка цепи). График зависимости мгновенной мощности от времени можно получить, перемножая значения силы тока и напряжения в каждый момент времени. Из этого графика видно, что в течение одной четверти периода мощность положительна и энергия поступает к данному участку цепи; но в течение следующей четверти периода мощность отрицательна, и данный участок отдает без потерь обратно в сеть полученную ранее энергию. Поступающая в течение четверти периода энергия запасается в магнитном поле тока, а затем без потерь возвращается в сеть.
(чисто индуктивное сопротивление участка цепи). График зависимости мгновенной мощности от времени можно получить, перемножая значения силы тока и напряжения в каждый момент времени. Из этого графика видно, что в течение одной четверти периода мощность положительна и энергия поступает к данному участку цепи; но в течение следующей четверти периода мощность отрицательна, и данный участок отдает без потерь обратно в сеть полученную ранее энергию. Поступающая в течение четверти периода энергия запасается в магнитном поле тока, а затем без потерь возвращается в сеть.