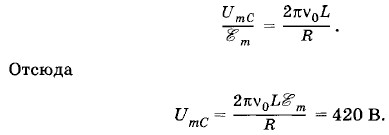|
|
|
|
|
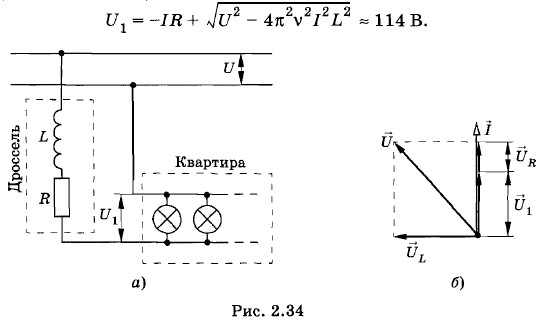
Глава 2. Электрические колебания 2.14. Примеры решения задач на тему: Электрические колебанияЗадача 4К магистрали переменного тока с напряжением U = 120 В (U — действующее значение напряжения) через катушку (дроссель) с индуктивностью L = 0,05 Гн и активным сопротивлением R = 1 Ом подключена осветительная сеть квартиры (рис. 2.34, а). Каково напряжение U1 на входе в квартиру, если сила потребляемого тока I = 2 А? Частота тока стандартная (ν = 50 Гц). Индуктивностью и емкостью электрической цепи квартиры пренебречь. Решение. Дроссель и осветительная сеть квартиры подключены к магистрали последовательно, поэтому сила тока одинакова на всех участках цепи. Напряжение U1 и напряжение UR на активном сопротивлении дросселя совпадают по фазе с силой тока I. Напряжение UL на индуктивном сопротивлении дросселя опережает силу тока по фазе на π/2. Следовательно, векторная диаграмма для действующих значений напряжений и силы тока имеет вид, изображенный на рисунке 2.34, б. По теореме Пифагора
где ω = 2πν. Так как действующее значение напряжения всегда положительно, то
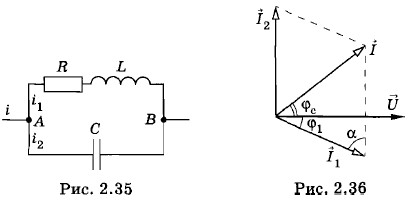
Задача 5В цепи (рис. 2.35) параметры R, L и С известны. Напряжение между точками А и В равно U. Постройте векторную диаграмму сил токов в данной цепи и определите силу тока в неразветвленном участке цепи. Найдите сдвиг фаз между колебаниями силы тока и напряжения. При каком условии сила тока в неразветвленном участке цепи окажется минимальной? Чему равен сдвиг фаз между силой тока и напряжением в этом случае? Решение. В этой задаче рассматривается электрическая цепь, состоящая из двух ветвей, соединенных параллельно. Одна ветвь содержит резистор и катушку индуктивности, другая — конденсатор. Построение векторной диаграммы начнем с вектора действующего значения напряжения
Поэтому вектор
Пользуясь теоремой косинусов, из векторной диаграммы определяем
Так как
Как видно из векторной диаграммы (см. рис. 2.36), вектор силы тока
Из выражения (2.14.1) вытекает, что сила тока в неразветвленном участке цепи минимальна, если LCω2 - 1 = 0, т. е. если При резонансе токов, как следует из формулы (2.14.2),
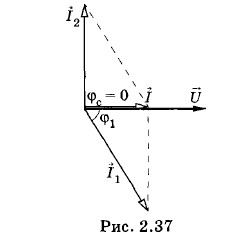
Это значит, что при резонансе токов при малом активном сопротивлении сдвиг фаз между силой тока и напряжением равен нулю (рис. 2.37). Важно обратить внимание на то, что при резонансе сила тока I в неразветвленной части цепи меньше силы тока I1 в ветви, содержащей последовательно соединенные резистор сопротивлением R и катушку индуктивностью L, а также меньше силы тока I2 в ветви с конденсатором емкостью С. Задача 6В колебательный контур (см. рис. 2.20) включен источник переменной ЭДС е = Решение. При резонансе амплитуда напряжения на конденсаторе, равная амплитуде напряжения на катушке UmL (UmC = UmL), больше амплитуды напряжения на зажимах цепи Um в отношении
|
|
|



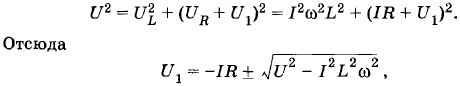
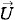 , поскольку напряжение одинаково для обеих ветвей цепи. Направим вектор
, поскольку напряжение одинаково для обеих ветвей цепи. Направим вектор 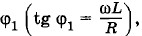 так как верхний участок цепи содержит катушку индуктивности.
так как верхний участок цепи содержит катушку индуктивности.
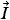 1 повернут относительно вектора
1 повернут относительно вектора 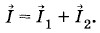
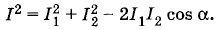
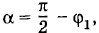 то cos α = sin φ1 и
то cos α = sin φ1 и
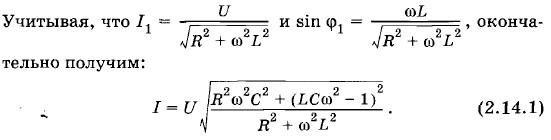
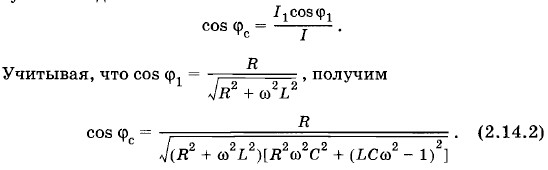
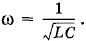 Но
Но 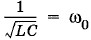 — это циклическая частота собственных колебаний контура, входящего в состав данной цепи. В этом случае говорят, что в цепи наступил резонанс токов.
— это циклическая частота собственных колебаний контура, входящего в состав данной цепи. В этом случае говорят, что в цепи наступил резонанс токов.
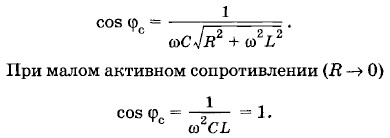
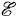 m cos ωt, причем амплитуда
m cos ωt, причем амплитуда 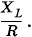 Если пренебречь внутренним сопротивлением источника переменной ЭДС, то Um =
Если пренебречь внутренним сопротивлением источника переменной ЭДС, то Um =