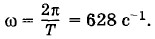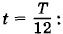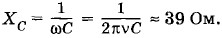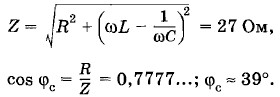|
|
|
|
|
Глава 2. Электрические колебания Примеры решения задач на тему: Электрические колебанияПри решении задач на электрические колебания рекомендуется учесть следующее. В задачах на свободные колебания в контуре, кроме формулы для периода свободных электрических колебаний (2.3.2), можно применять закон сохранения энергии. При решении задач на расчет цепей переменного тока следует иметь в виду, что амперметры и вольтметры в этих цепях показывают действующие значения силы тока (2.5.4) и действующие значения напряжения (2.5.5). В отличие от цепей постоянного тока, обладающих только активным сопротивлением, цепи переменного тока могут иметь еще емкостное сопротивление (2.7.4) и индуктивное сопротивление (2.8.5). Полное сопротивление цепи с последовательно соединенными резистором, конденсатором и катушкой индуктивности определяется по формуле (2.9.4). Закон Ома для цепи переменного тока имеет вид (2.9.5). При последовательном соединении потребителей в цепях переменного тока действующие или амплитудные значения напряжений складываются методом векторной диаграммы. При параллельном соединении потребителей в цепях переменного тока векторно складываются амплитуды сил токов или их действующие значения. В этом случае тоже следует строить векторные диаграммы. При построении векторных диаграмм надо хорошо знать фазовые соотношения между колебаниями силы тока и напряжения в цепях переменного тока. Мощность вычисляется по формуле (2.10.4). Явление резонанса в электрической цепи имеет место при условии (2.11.1). Задача 1Колебательный контур состоит из катушки индуктивностью L = 6 • 10-3 Гн и конденсатора емкостью С = 15 мкФ. Максимальная разность потенциалов на конденсаторе Um = 200 В. Чему равна сила тока i в контуре, когда разность потенциалов на конденсаторе уменьшилась в n = 2 раза? Потерями энергии пренебречь. Решение. Когда напряжение на обкладках конденсатора максимально, вся энергия контура сосредоточена в электрическом поле конденсатора (см. § 2.2.). Она равна Согласно закону сохранения энергии имеем:
Задача 2Напряжение на концах участка цепи, по которому течет переменный ток, изменяется с течением времени по закону Решение. Сначала найдем значение циклической частоты:
Далее записываем выражение для мгновенного значения напряжения в момент времени
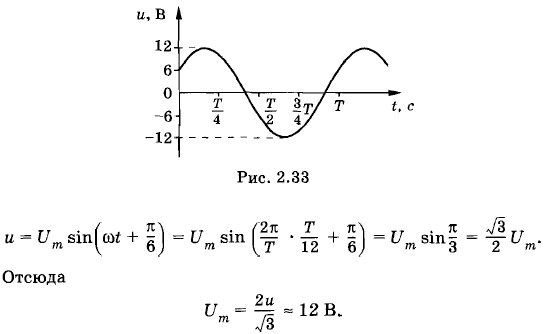
График изменения напряжения в зависимости от времени представлен на рисунке 2.33. Задача 3В цепь переменного тока стандартной частоты (ν = 50 Гц) последовательно включены резистор сопротивлением R = 21 Ом, катушка индуктивностью L = 0,07 Гн и конденсатор емкостью С = 82 мкФ (см. рис. 2.20). Определите индуктивное, емкостное и полное сопротивления цепи, а также сдвиг фаз между силой тока и напряжением. Решение. Индуктивное сопротивление находим по формуле (2.8.5): XL = ωL = 2πνL = 22 Ом. Емкостное сопротивление вычисляется по формуле (2.7.4):
Полное сопротивление согласно формуле (2.9.4) равно:
|
|
|



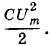 При уменьшении напряжения на обкладках конденсатора до значения
При уменьшении напряжения на обкладках конденсатора до значения 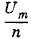 энергия контура распределяется между конденсатором и катушкой. Энергия электрического поля конденсатора становится равной
энергия контура распределяется между конденсатором и катушкой. Энергия электрического поля конденсатора становится равной 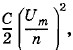 а энергия магнитного поля катушки будет равна
а энергия магнитного поля катушки будет равна 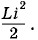
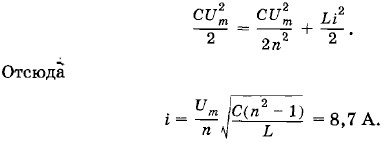
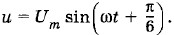 В момент времени
В момент времени 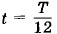 мгновенное значение напряжения u = 10 В. Определите амплитуду напряжения Um и циклическую частоту ω, если период колебаний силы тока Т = 0,01 с. Начертите график зависимости изменения напряжения от времени.
мгновенное значение напряжения u = 10 В. Определите амплитуду напряжения Um и циклическую частоту ω, если период колебаний силы тока Т = 0,01 с. Начертите график зависимости изменения напряжения от времени.