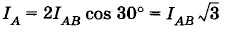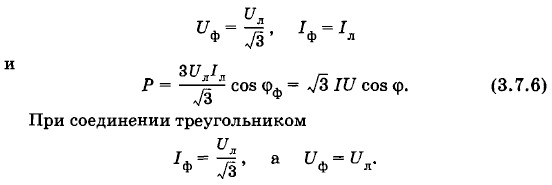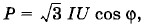|
|
|
|
|
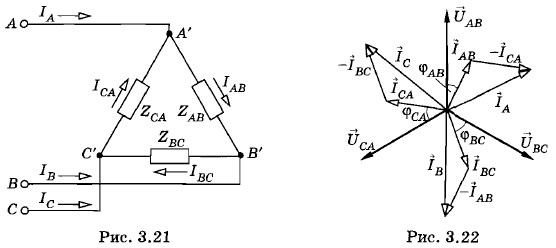
Глава 3. Производство, передача, распределение и использование электрической энергии Соединение потребителей электрической энергииСоединение треугольникомПри соединении потребителей электроэнергии треугольником (рис. 3.21) отдельные фазы нагрузки присоединяются к линейным проводам, идущим от генератора. Следовательно, каждая фаза нагрузки находится под линейным напряжением. Токи, текущие по отдельным фазам нагрузки (IAB, IBC, ICA ) называются фазными токами, а токи, текущие по линейным проводам от генератора к нагрузке (IА, IВ, IС), называются линейными токами. Найдем зависимость между линейными и фазными токами при соединении нагрузки треугольником. Выберем положительное направление фазных токов от А' к В', от В' к С' и от С' к А' (см. рис. 3.21). За положительное направление линейных токов принимаем, как и раньше, направление от генератора к нагрузке. Для мгновенных значений сил токов, сходящихся в точке А', по первому правилу Кирхгофа имеем: iA + iCA = iAB. Отсюда iА = iАВ - iСА.
Аналогично для точки В': iB = iBC - iBC. iС = iСА - iВС. Действующие значения сил линейных токов находятся как геометрические разности векторов соответствующих фазных токов:
На рисунке 3.22 изображена векторная диаграмма для действующих значений линейных напряжений и сил фазных токов при соединении потребителей энергии треугольником в случае неравномерной индуктивно-активной нагрузки. На этой диаграмме видно, что силы фазных токов отстают по фазе от соответствующих линейных напряжений (векторы сил токов повернуты относительно векторов напряжений по часовой стрелке), причем φАВ ≠ φВС ≠ φСА. Длины векторов сил фазных токов При симметричной нагрузке, включенной по схеме треугольника (см. рис. 3.21), между действующими значениями сил фазных и линейных токов выполняется соотношение
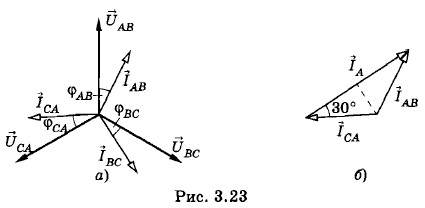
В этом можно убедиться, рассмотрев векторную диаграмму, изображенную на рисунке 3.23, а. На этой векторной диаграмме в отличие от векторной диаграммы, изображенной на рисунке 3.22, векторы сил фазных токов
Определим силу линейного тока IА. Для этого согласно равенствам (3.7.3) надо найти разность векторов
Мощность трехфазной системыМощность одной фазы Рф = UфIф cos φф. При равномерной (симметричной) нагрузке мощность трех фаз Р = ЗРф = ЗUфIф cos φф. (3.7.5) Когда нагрузки соединены звездой, то
Подставив эти значения Iф и Uф в формулу (3.7.5), снова получим выражение (3.7.6). Итак, мощность трехфазной системы
где под I и U надо понимать действующие значения линейных токов и напряжений. При неравномерной нагрузке фаз мощность трехфазной системы определяется как сумма мощностей отдельных фаз: Р = РА + РВ + РC.
|
|
|



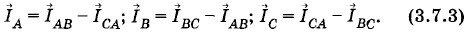
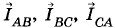 тоже различны. Все это из-за несимметричности нагрузки на фазы.
тоже различны. Все это из-за несимметричности нагрузки на фазы.

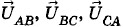 на одинаковые углы (φAB = φВС = φСА).
на одинаковые углы (φAB = φВС = φСА).
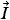 AB -
AB -