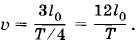§ 4.2. Поперечные волны

Рассмотрим процесс распространения волны более детально. Проследим за движением отдельных частиц вещества при волновом движении. Сначала рассмотрим поперечную волну, такую, например, которая распространяется вдоль резинового шнура.

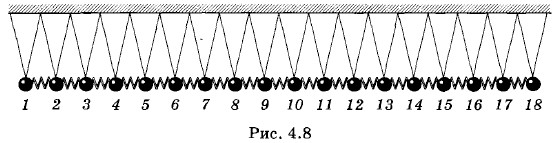
Проще всего иметь дело не с самим резиновым шнуром, а с его упрощенной моделью.

Каждый участок шнура обладает массой и упругостью. При деформации шнура в каждом его сечении появляются силы упругости. Вместо реального шнура возьмем цепочку одинаковых металлических шаров, подвешенных на нитях. Шары связаны между собой пружинами (рис. 4.8). Масса пружин много меньше массы шаров. В этой модели инертные (масса) и упругие свойства шнура разделены: масса сосредоточена в основном в шарах, а упругость — в пружинах. Это разделение несущественно при исследовании волнового движения.

Шары связаны между собой пружинами

Если отклонить левый крайний шар в горизонтальной плоскости, то пружина деформируется, и на шар 2 начнет действовать сила, заставляя его отклоняться в ту же сторону, в которую был отклонен шар 1. Чем больше масса шара, тем медленнее он будет набирать скорость под действием силы. Вследствие этого движение шара 2 не будет происходить согласованно с движением шара 1. Чем больше массы шаров, тем больше шар 2 отстает в своем движении от шара 1. Существенна здесь еще и жесткость пружины. Чем больше жесткость пружины, тем больше сила упругости при данной деформации и, следовательно, шар 2 быстрее будет набирать скорость. Его движение, повторяющее движение шара 1, меньше будет запаздывать по времени.

Если шар 1 заставить совершать периодическое движение (просто рукой или с помощью какого-либо механизма, превращающего вращательное движение в колебательное), то шар 2 тоже придет в колебательное движение вслед за шаром 1, но с некоторым отставанием по фазе. Шар 3 под влиянием силы упругости, действующей на него со стороны шара 2, тоже начнет колебаться, еще более отставая по фазе, и т. д. Наконец, все шары станут колебаться с одной и той же частотой, но с различными фазами. При этом вдоль цепочки шаров побежит поперечная волна. Проследим, как она образуется.

Пусть, к примеру, цепочка содержит 18 шаров. В начальный момент все они покоятся (рис. 4.9, а). Шар 1 приводится в колебательное движение с периодом Т и амплитудой s_m. По истечении времени 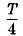он отклонится от положения равновесия на расстояние s_m. При этом он вовлекает в движение шар 2, а шар 2 вовлекает шар 3 и т. д. Когда шар 1 достигает максимального отклонения от положения равновесия, шар 2 его еще не достигнет, а шар 3 сместится от положения равновесия лишь на небольшое расстояние, шар 4 вообще еще не успеет сдвинуться с места (рис. 4.9, б). В момент времени 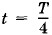он только начнет движение. На рисунке 4.9, б и на всех последующих стрелки у шаров — это векторы скорости движения шаров в соответствующие моменты времени (вид сверху). Конечно, совсем не обязательно, чтобы именно шар 4 начинал свое движение спустя четверть периода. Это может быть и шар 5, и шар 6 или еще более далекий шар. Все зависит от масс шаров и упругости пружин, так как именно они определяют скорость распространения колебаний. Мы лишь условно считаем, что в рассматриваемой модели колебания за время распространяются от шара 1 до шара 4. Если расстояние между соседними шарами l₀, то скорость распространения колебании равна

Если подобным образом проследить далее за распространением колебаний (рис. 4.9, в, г), то можно убедиться в том, что спустя время Т после начала процесса шар 1 окажется опять в положении равновесия, а колебания уже достигнут шара 13 (рис. 4.9, д). После этого начнется второй период колебаний (рис. 4.9, е).