|
|
|
|
|
Глава 4. Механические волны. Звук § 4.4. Продольные волны
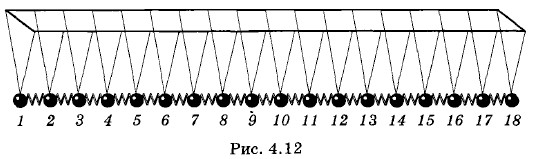
Пусть шар 1 приведен в колебательное движение с периодом Т и амплитудой sm. Спустя четверть периода он сместится вправо на расстояние sm и с помощью пружины приведет в движение шар 2, который, в свою очередь, заставит двигаться шар 3, и т. д. Но шар 2 начнет движение позднее шара 1, шар 3 позднее шара 2 и т. д. Поэтому, когда шар 1 сместится на расстояние sm, шар 2 сместится от своего положения равновесия на меньшее расстояние, шар 3 — еще на меньшее, а шар 4 и все последующие вообще пока не начнут двигаться. В результате шары займут положение, указанное на рисунке 4.13, б.
По истечении промежутка времени Следя далее за движением шаров, мы убеждаемся в том, что спустя период Т шар 1 не только окажется в положении равновесия, но и будет двигаться в том же направлении, что и в самом начале. Колебания же успеют распространиться до шара 13 (рис. 4.13, д). Опять мы, как и в случае поперечной волны, изображенной на рисунке 4.9, имеем волну, бегущую направо. Но теперь эта волна состоит из чередующихся уплотнений и разрежений пружин с шарами. Длина волны равна расстоянию между серединами двух соседних уплотнений или разрежений. Шары 1 и 13 колеблются с одинаковыми фазами. Расстояние между ними как раз равно длине волны. То же самое можно сказать о шарах 2 и 14, 3 и 15 и т. д. (рис. 4.13, е). Для скорости продольной волны справедлива та же формула (4.3.2), что и в случае поперечной волны: υ = λν.
|
|
|




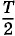 после начала движения шар 1 опять окажется в положении равновесия, но будет двигаться уже влево (рис. 4.13, в). Через промежуток времени, равный
после начала движения шар 1 опять окажется в положении равновесия, но будет двигаться уже влево (рис. 4.13, в). Через промежуток времени, равный  шар 1 будет максимально отклонен влево от положения равновесия (рис. 4.13, г).
шар 1 будет максимально отклонен влево от положения равновесия (рис. 4.13, г).