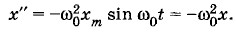|
|
|
|
|
Глава 1. Механические колебания § 1.4. Гармонические колебания
Ускорение — вторая производная координаты по времениМгновенная скорость, как известно из курса математики, представляет собой производную координаты по времени. Ускорение — это производная скорости по времени, или вторая производная координаты по времени*. Поэтому уравнение (1.2.6), описывающее колебания груза на пружине, можно записать так: * Для краткости мы говорим об ускорении и скорости. В действительности имеются в виду проекции этих величин.
где х" — вторая производная координаты по времени. Согласно уравнению (1.4.1) при свободных колебаниях координата х изменяется со временем так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку. Гармонические колебанияИз курса математики известно, что функции синус и косинус обладают тем свойством, что вторая производная функции пропорциональна самой функции, взятой с противоположным знаком. Можно доказать, что никакие другие функции этим свойством не обладают. Значит, координата тела, совершающего свободные колебания, меняется с течением времени по закону синуса или косинуса. Когда тело совершает колебания, его движения периодически повторяются. Поэтому неудивительно, что изменение co временем координаты тела выражается через периодические функции синус или косинус. Периодические изменения физической величины в зависимости от времени по закону синуса или косинуса называются гармоническими колебаниями. Амплитуда колебанийВажной характеристикой колебательного движения является амплитуда. Амплитудой гармонических колебаний называется модуль наибольшего смещения тела от положения равновесия. Амплитуда может иметь различные значения в зависимости от того, насколько мы смещаем тело от положения равновесия в начальный момент времени, и от того, какая скорость сообщается при этом телу. Амплитуда определяется начальными условиями. Но максимальные значения модуля синуса и косинуса равны единице. Поэтому решение уравнения (1.4.1) не может просто выражаться косинусом или синусом. Оно должно иметь вид произведения амплитуды хm на синус или косинус. Решение уравнения движения, описывающего свободные колебанияКакую же форму имеет решение уравнения (1.7.1)? Нельзя просто считать, что х = хm sin t или х = хm cos t, так как в этом случае вместо х" = - Но небольшое усложнение формы решения сразу приведет нас к цели. Чтобы в выражении второй производной x"(t) был множитель х = хm sin ω0t. (1-4.2) В этом случае первая производная (скорость) принимает вид: х' = ω0хm cos ω0t, а вторая производная (ускорение) равна:
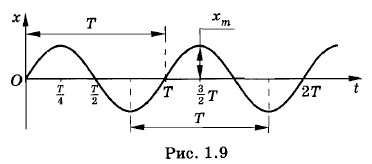
Мы в точности получили уравнение (1.4.1). Следовательно, функция (1.4.2) есть решение исходного уравнения (1.4.1). Конечно, решением исходного уравнения будет также функция: х = хm cos ω0t. График зависимости координаты тела от времени согласно уравнению (1.4.2) представляет собой синусоиду, изображенную на рисунке 1.9.
Но выражение (1.4.2) — это еще не самое общее решение уравнения (1.4.1). Нетрудно убедиться, что решением уравнения (1.4.1) будет также синус или косинус, если к их аргументу добавить произвольную постоянную величину φ0:
Постоянная величина φ0 не определяется уравнением (1.4.1). В дальнейшем мы покажем, что подобно амплитуде колебаний она определяется начальными условиями. Функция x = хm cos (ω0t + φ0) (1-4.4) также является решением уравнения (1.4.1).
|
|
|




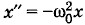 X получилось бы равенство х" = -xm sin t = -х.
X получилось бы равенство х" = -xm sin t = -х.
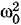 , запишем решение уравнения (1.4.1) в следующем виде:
, запишем решение уравнения (1.4.1) в следующем виде: