|
|
|
|
|
Глава 1. Механические колебания § 1.3. Уравнение движения математического маятникаРассмотрим простой маятник — шарик, подвешенный на длинной прочной нити. Если размеры шарика много меньше длины нити, то этими размерами можно пренебречь и рассматривать шарик как материальную точку. Растяжением нити также можно пренебречь, так как оно очень мало. Можно пренебречь и ее массой по сравнению с массой шарика. Таким образом, вместо реального маятника — шарика определенного размера на нити, которая, конечно, немного деформируется при движении и имеет массу, мы вправе рассматривать простую модель: материальную точку, подвешенную на нерастяжимой невесомой нити. Такая модель маятника называется математическим маятником в отличие от реального маятника, называемого физическим. Маленький шарик на длинной тонкой нити должен вести себя практически так же, как и математический маятник. Выведем маятник из положения равновесия и отпустим. На шарик будут действовать две силы: сила тяжести Силу тяжести Тангенциальная составляющая
При колебаниях шарика на нерастяжимой нити он всегда движется по дуге окружности, радиус которой равен длине нити l. Поэтому положение шарика в любой момент определяется одной величиной — углом α отклонения нити от вертикали (см. рис. 1.8). Будем считать угол α положительным, если маятник отклонен вправо от положения равновесия, и отрицательным, если он отклонен влево. Уравнение для тангенциальной составляющей ускоренияТангенциальная проекция силы тяжести в момент, когда нить маятника отклонена от положения равновесия на угол а, выражается так: Fτ = -F sin α = -mg sin α. (1.3.1) (Мы считаем значение проекции положительным, если составляющая силы направлена слева направо.) Знак «-» в уравнении (1.3.1) стоит из-за того, что Fτ и α имеют противоположные знаки. При отклонении маятника вправо (α > 0) составляющая Согласно второму закону Ньютона mаτ = Fτ, или mаτ =-mg sin α. (1.3.2) Разделив левую и правую части этого уравнения на т, получим: аτ =-g sin α. (1.3.3) До сих пор считалось, что углы отклонения нити от вертикали могут быть любыми. В дальнейшем будем считать их малыми. При малых углах, если выражать угол α в радианах, sin α ≈ α. Следовательно, aτ = -gα. (1.3.4) Смещение шарика маятника от положения равновесия можно характеризовать не только углом, но и величиной, измеряемой длиной дуги ОА (см. рис. 1.8), взятой со знаком «+», если шарик смещается от положения равновесия вправо, и со знаком «-», если он смещается влево. Очевидно, что
где s — длина дуги ОА. Подставив в уравнение (1.3.4) это значение α, получим:
Введя обозначение
приходим к окончательному виду уравнения движения маятника при малых углах отклонения от положения равновесия:
Это уравнение имеет такой же вид, как и уравнение (1.2.6) движения шарика, прикрепленного к пружине. Здесь только вместо проекции ускорения аx стоит тангенциальное ускорение аτ и вместо координаты х — величина s. Да и Важное заключение. Мы пришли к замечательному выводу: уравнения движения, описывающие колебания таких различных систем, как груз на пружине и маятник, одинаковы. Это означает, что движение шарика и колебания маятника происходят одинаковым образом. Смещения груза на пружине и шарика маятника от положения равновесия изменяются со временем по одному и тому же закону, несмотря на то, что силы, вызывающие колебания, имеют различную физическую природу. В первом случае это сила упругости, а во втором — составляющая силы тяжести. Уравнение движения (1.2.6), как и уравнение (1.3.8), выглядит внешне очень просто: ускорение прямо пропорционально координате. Но решить его, т. е. определить, как меняется координата колеблющегося тела с течением времена, не просто. До сих пор в механике мы в основном рассматривали движение с постоянным ускорением. При колебаниях же ускорение меняется со временем, так как меняется сила, действующая на тело.
|
|
|



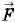 = m
= m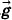 , направленная вертикально вниз, и сила упругости нити
, направленная вертикально вниз, и сила упругости нити 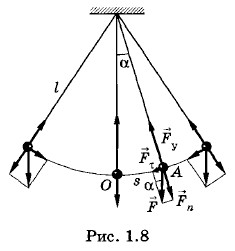




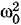 зависит уже не от жесткости пружины и массы груза, а от ускорения свободного падения и длины нити. Но по-прежнему ускорение прямо пропорционально смещению (определяемому дугой) шарика от положения равновесия. Если бы мы в случае маятника обозначили тангенциальное ускорение через аx, а дугу через х, то оба уравнения (1.2.6) и (1.3.8) были бы неразличимы.
зависит уже не от жесткости пружины и массы груза, а от ускорения свободного падения и длины нити. Но по-прежнему ускорение прямо пропорционально смещению (определяемому дугой) шарика от положения равновесия. Если бы мы в случае маятника обозначили тангенциальное ускорение через аx, а дугу через х, то оба уравнения (1.2.6) и (1.3.8) были бы неразличимы.