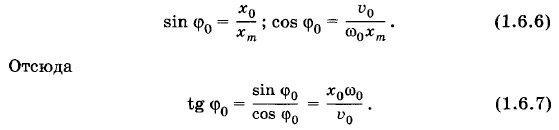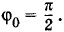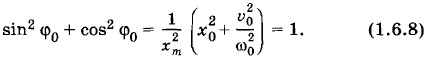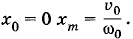|
|
|
|
|
Глава 1. Механические колебания § 1.6. Фаза колебаний. Определение амплитуды и начальной фазы из начальных условийФаза колебанийПри заданной амплитуде гармонических колебаний координата колеблющегося тела в любой момент времени однозначно определяется аргументом синуса или косинуса, равным φ = ω0t + φ0 [формулы (1.4.3) и (1.4.4)]. Величину φ, стоящую под знаком синуса или косинуса, называют фазой* колебаний, описываемых этими функциями. Выражается фаза в угловых единицах — радианах или градусах. * От греческого слова phasis — появление, ступень развития какого-либо явления. Фаза определяет не только координаты, но и другие физические величины, например скорости и ускорения, изменяющиеся по гармоническому закону. Начальная фаза. Сдвиг фазВ начальный момент времени t = 0 фаза φ = ω0t + φ0 (1.6.1) имеет значение φ0. Это значение фазы называется начальной фазой. Два или несколько гармонических колебаний с одинаковыми частотами и амплитудами могут отличаться друг от друга только начальными фазами. Между колебаниями имеется разность фаз, или, как часто говорят, сдвиг фаз φс. Если начальная фаза первого колебания равна φ01, а второго φ02, то сдвиг фаз второго колебания относительно первого равен: φc = φ02 - φ01. (1.6.2)
На рисунке 1.10 изображены графики колебаний, сдвинутых по фазе на x1 = хm sin ω0t График 2 соответствует колебаниям, сдвинутым по фазе на
Начальная фаза этих колебаний Так как x2 = xm cos ω0t. Таким образом, колебания, описываемые синусом и косинусом, представляют собой колебания со сдвигом фаз Определение амплитуды и начальной фазы из начальных условийУже упоминалось, что амплитуда и начальная фаза не определяются уравнением движения. Их значения зависят от начальной координаты х(0) = х0 и начальной скорости х'(0) = υ0. Значения x0 и υ0 определяются условиями возбуждения колебаний. Если вывести тело из положения равновесия и отпустить, не сообщая ему скорости, то х(0) = х0, а х'(0) = 0. Напротив, если сообщить телу начальную скорость, толкнув его в положении равновесия, то х(0) = 0, а х'(0) = υ0. Рассмотрим общий случай, когда при t = 0 х(0) ≠ 0 и х'(0) ≠ 0. Выбор решения в форме синуса или косинуса повлияет на начальную фазу, но не на амплитуду. Пусть решение уравнения (1.4.1) имеет вид: х = хm sin (ω0t + φ0). (1.6.3) Тогда х' = ω0хm cos (ω0t + φ0). (1.6.4) При t = 0
Согласно уравнениям (1.6.5)
Это выражение определяет начальную фазу φ0. В частном случае, если x0 = 0, то tg φ0 = 0 и φ0 = 0. Если же υ0 = 0, то tg φ0 = ∞ и Возведя в квадрат оба уравнения (1.6.6) и сложив их левые и правые части, получим:
Отсюда амплитуда колебаний
При υ0 = 0 хm = х0, а при Если бы мы выразили решение не через синус, а через косинус, то амплитуда по-прежнему имела бы значение, определяемое формулой (1.6.9), а начальная фаза определялась бы уравнением
Получите это выражение самостоятельно и рассмотрите предельные случаи x0 = 0 и υ0 = 0.
|
|
|



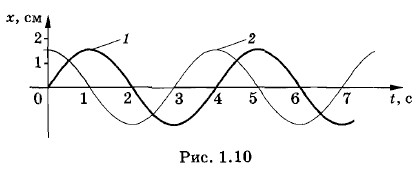
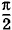 . График 1 соответствует колебаниям, совершающимся по синусоидальному закону с начальной фазой, равной нулю (φ01 = 0):
. График 1 соответствует колебаниям, совершающимся по синусоидальному закону с начальной фазой, равной нулю (φ01 = 0):
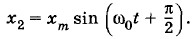
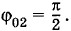
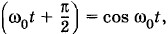 то
то