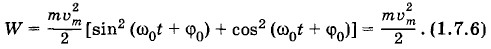|
|
|
|
|
Глава 1. Механические колебания § 1.7. Скорость и ускорение при гармонических колебаниях. Превращения энергии
СкоростьПроекция скорости на ось X есть производная координаты по времени. Если х = хm cos (ω0t + φ0), то
Скорость при гармонических колебаниях меняется с течением времени гармонически. Амплитуда скорости равна υm = ω0хm, а по фазе колебания скорости опережают колебания координаты к на В момент, когда координата равна нулю (момент прохождения положения равновесия), модуль скорости максимален, и, наоборот, скорость равна нулю, когда координата максимальна по модулю (рис. 1.11, а, б; φ0 = 0). УскорениеПроекция ускорения на ось X есть производная скорости по времени:
Ускорение при гармонических колебаниях координаты меняется гармонически. Амплитуда ускорения равна Ускорение и координата одновременно становятся максимальными по модулю, но имеют противоположные знаки. В подобных случаях говорят, что колебания происходят в противофазе (рис. 1.11, а, в; φ0 = 0). Относительно колебаний скорости колебания ускорения сдвинуты по фазе на Превращения энергии при гармонических колебанияхОттянув груз, подвешенный на пружине, вниз, мы сообщаем грузу некоторый запас потенциальной энергии. При движении груза вверх пружина сокращается и потенциальная энергия уменьшается. Но одновременно увеличивается кинетическая энергия груза. В момент прохождения телом положения равновесия потенциальная энергия становится минимальной. Кинетическая же энергия достигает максимума. После прохождения положения равновесия скорость начинает уменьшаться. Следовательно, уменьшается и кинетическая энергия. Потенциальная энергия снова растет. В самой верхней точке она достигает максимума, а кинетическая энергия становится равной нулю. Таким образом, при колебаниях периодически происходит переход потенциальной энергии в кинетическую и обратно. Частота колебаний потенциальной и кинетической энергий в два раза больше частоты колебаний тела. Такие же изменения кинетической и потенциальной энергий происходят при колебаниях маятника. Полная механическая энергия при колебаниях груза на пружине равна сумме кинетической и потенциальной энергий:
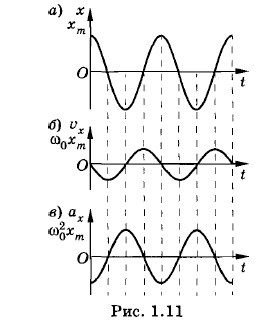
Кинетическая и потенциальная энергии периодически изменяются, но полная механическая энергия в системе без трения согласно закону сохранения энергии остается неизменной. Она равна либо потенциальной энергии в момент максимального отклонения от положения равновесия, либо кинетической энергии в момент, когда тело проходит положение равновесия. Докажем это. Подставим в формулу (1.7.3) выражения для υx и х:
Заменив в первом члене уравнения (1.7.4)
Если же во второй член уравнения (1.7.4) подставить
|
|
|



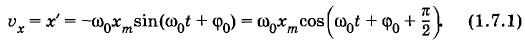
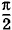 .
.
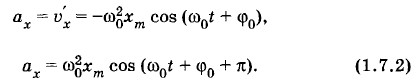
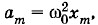 а по фазе колебания ускорения опережают колебания координаты на π.
а по фазе колебания ускорения опережают колебания координаты на π.
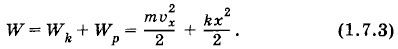
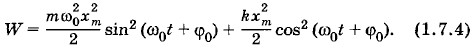
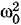 его значением
его значением 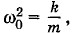 получим:
получим:
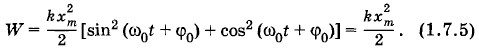
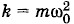 и учесть, что (ω0хm = υm, то будем иметь:
и учесть, что (ω0хm = υm, то будем иметь: