|
|
|
|
|
Глава 5. Электромагнитные волны § 5.5. Классическая теория излучения
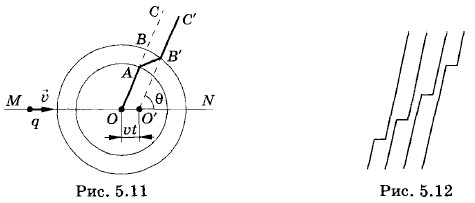
Напряженность электрического поля заряда, движущегося с ускорениемРассмотрим электрический заряд q, движущийся с постоянной скоростью υ << с вдоль прямой MN. В некоторый момент времени заряд начинает тормозиться и за очень малое время т останавливается в точке О (рис. 5.11) в момент времени t0 = 0. Когда заряд движется с постоянной скоростью, его «сопровождает» электрическое поле, силовые линии которого представляют собой прямые, начинающиеся на заряде. Одна из таких линий ОС, составляющая угол θ с направлением движения заряда, изображена на рисунке 5.11. При торможении заряда силовые линии начинают деформироваться, так как электромагнитные взаимодействия распространяются с конечной скоростью с, и удаленные участки силовых линий при торможении заряда сразу не меняются и продолжают перемещаться так, как если бы заряд двигался по-прежнему равномерно. В результате ускорения силовые линии возле заряда изгибаются, и этот изгиб со скоростью с перемещается вдоль силовой линии. При остановке заряда его кулоновское поле восстанавливается вначале в окрестности заряда, а затем постепенно во всем окружающем пространстве. На рисунке 5.12 представлена примерная форма силовой линии в различные моменты времени.
Если заряд останавливается спустя время т после начала торможения, то за время t - τ его кулоновское поле восстанавливается внутри сферы радиусом c(t - τ). На рисунке 5.11 показана силовая линия ОА внутри этой сферы. Вне сферы радиусом r = ct силовые линии еще не успевают деформироваться. В момент времени t силовая линия изображена отрезком В'С'. Такое положение силовая линия имела бы, если бы торможения не происходило. Заряд за это время сместился бы относительно точки, где началось торможение, на отрезок υ(t + τ). Будем считать t >> τ. Тогда это расстояние примерно равнялось бы υt = ОО' (см. рис. 5.11). Силовая линия имела бы форму луча О'С'. Изгиб силовой линии АВ' означает появление у ускоренно движущегося заряда составляющей напряженности электрического поля, перпендикулярной радиусу, соединяющему данную точку поля с зарядом. Это и есть вихревое электрическое поле электромагнитной волны. Вычислим напряженность этого (поперечного) поля. Направление силовой линии на участке АВ' совпадает с направлением напряженности
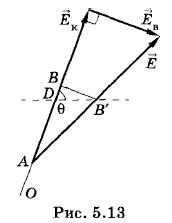
Вследствие того, что υ << с и τ мало, дугу ВВ' можно рассматривать как отрезок прямой (см. рис. 5.11). Прямоугольный треугольник векторов напряженностей
Согласно построению (см. рис. 5.11, 5.13)
где r — радиус сферы ОВ. С учетом этих соотношений и выражения (5.5.1) из уравнения (5.5.2) получим:
Отношение
Полученное выражение совершенно справедливо и вытекает из уравнений Максвелла при скорости движения υ << с. Оно оказывается правильным для всех случаев ускоренного движения заряда, а не только при торможении*. Любое ускорение заряда сопровождается излучением электромагнитной волны. * Отметим, что напряженность вихревого поля волны на расстоянии r от излучающей частицы определяется ускорением в более ранний момент времени Возникает естественный вопрос: как же удалось получить правильный общий результат, не учитывая ни порождения электрического поля магнитным, ни обратного процесса порождения магнитного поля переменным электрическим полем? На самом деле эти процессы неявно были учтены. В наших рассуждениях было принято, что электромагнитные возмущения распространяются с конечной скоростью с. Этот факт не был нами теоретически обоснован. Он является следствием уравнений Максвелла и вытекает из существования упомянутых выше процессов. Большим недостатком данного упрощенного рассмотрения является то, что с его помощью нельзя получить значение другой характеристики поля — магнитной индукции. Оказывается, что магнитная индукция волны определяется такой же формулой, что и напряженность электрического поля:
Вектор Взаимодействие посредством электромагнитных волнСамым замечательным в формулах (5.5.4) и (5.5.5) является медленность убывания напряженности электрического поля и индукции магнитного поля электромагнитной волны с расстоянием. Напряженность кулоновского поля и индукция магнитного поля постоянных токов убывают с расстоянием как Все другие силы убывают с расстоянием гораздо быстрее. Вот почему электромагнитные поля, излучаемые даже сравнительно маломощной радиостанцией, могут быть обнаружены на расстояниях в тысячи километров, в то время как стационарные поля на таких расстояниях уже никак не проявляются.
|
|
|



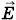 электрического поля (рис. 5.13). Эту напряженность можно рассматривать как сумму двух векторов: напряженности
электрического поля (рис. 5.13). Эту напряженность можно рассматривать как сумму двух векторов: напряженности 

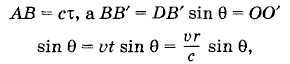

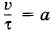 представляет собой модуль ускорения заряда при торможении. Следовательно, окончательно выражение для напряженности вихревого электрического поля электромагнитной волны в системе Гаусса будет иметь вид:
представляет собой модуль ускорения заряда при торможении. Следовательно, окончательно выражение для напряженности вихревого электрического поля электромагнитной волны в системе Гаусса будет иметь вид:

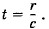

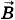 в направлен перпендикулярно вектору
в направлен перпендикулярно вектору 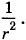 И при этом кулоновские и магнитные силы считаются r дальнодействующими подобно гравитационным. Напряженность электрического поля и индукция магнитного поля, пропорциональные ускорению зарядов, убывают в пространстве пропорционально
И при этом кулоновские и магнитные силы считаются r дальнодействующими подобно гравитационным. Напряженность электрического поля и индукция магнитного поля, пропорциональные ускорению зарядов, убывают в пространстве пропорционально 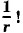 Это крайне медленное убывание.
Это крайне медленное убывание.