|
|
|
|
|
Глава 5. Электромагнитные волны § 5.6. Энергия электромагнитной волныПлотность энергии излученияФормулы (5.5.4) и (5.5.5) для модулей Е и В* позволяют определить плотность энергии электромагнитного излучения. * Мы не ставим индекс «в» у векторов Плотность энергии электрического поля в системе Гаусса равна (в вакууме):
Плотность энергии магнитного поля определяется аналогичной формулой:
Полная плотность энергии электромагнитной волны
Плотность потока излученияОт заряженных частиц, движущихся ускоренно, излучение распространяется во все стороны. Наряду с плотностью энергии вводят еще одну энергетическую характеристику излучения: плотность потока электромагнитного излучения. Плотностью потока электромагнитного излучения I называют отношение электромагнитной энергии W, прошедшей за время Δt через перпендикулярную к направлению распространения волны поверхность площадью S, к произведению площади S на время Δt:
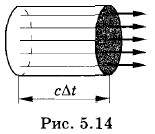
Плотность потока излучения простым образом связана с плотностью энергии электромагнитной волны. Выберем поверхность площадью S, перпендикулярную лучам, и построим на ней как на основании цилиндр с образующей с Δt (рис. 5.14). Объем цилиндра ΔV = ScΔt. Энергия электромагнитного поля внутри цилиндра равна произведению плотности энергии на объем:
Вся эта энергия за время Δt пройдет через правое основание цилиндра. Поэтому из (5.6.4) получаем
т. е. плотность потока излучения равна произведению плотности энергии на скорость ее распространения. Плотность потока излучения в среднем за период представляет собой мощность излучения, проходящего через единичную площадку. Иногда ее называют интенсивностью излучения. Эта величина с учетом выражения (5.6.3) равна:
Плотность потока излучения по мере удаления от источника убывает как
|
|
|



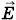 и
и 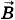 , так как здесь и далее имеется в виду только электромагнитное поле волны.
, так как здесь и далее имеется в виду только электромагнитное поле волны.


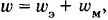





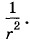 Согласно закону сохранения энергии так и должно быть. Если окружить излучающие заряды сферической поверхностью, то полный поток излучения через эту поверхность не должен зависеть от ее радиуса. Мы ведь рассматриваем излучение в вакууме, где поглощения энергии не происходит. Но площадь сферы пропорциональна квадрату ее радиуса. Поэтому плотность потока излучения (т. е. мощность, приходящаяся на единицу площади) должна быть обратно пропорциональна квадрату радиуса.
Согласно закону сохранения энергии так и должно быть. Если окружить излучающие заряды сферической поверхностью, то полный поток излучения через эту поверхность не должен зависеть от ее радиуса. Мы ведь рассматриваем излучение в вакууме, где поглощения энергии не происходит. Но площадь сферы пропорциональна квадрату ее радиуса. Поэтому плотность потока излучения (т. е. мощность, приходящаяся на единицу площади) должна быть обратно пропорциональна квадрату радиуса.