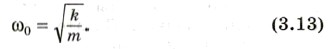|
|
|
|
|
Глава 3. Механические колебания Гармонические колебанияАмплитуда колебанийАмплитудой гармонических колебаний называется модуль наибольшего смещения тела от положения равновесия. Амплитуда может иметь различные значения в зависимости от того, насколько мы смещаем тело от положения равновесия в начальный момент времени, или от того, какая скорость сообщается телу. Амплитуда определяется начальными условиями, а точнее энергией, сообщаемой телу. Но максимальные значения модуля синуса и модуля косинуса равны единице. Поэтому решение уравнения (3.11) не может выражаться просто синусом или косинусом. Оно должно иметь вид произведения амплитуды колебаний хт на синус или косинус. Р е ш е н и е уравнения, описывающего свободные колебания. Запишем решение уравнения (3.11) в следующем виде:
В этом случае первая производная принимает вид
а вторая производная будет равна:
Мы получили уравнение (3.11). Следовательно, функция (3.12) есть решение исходного уравнения (3.11). Решением этого уравнения будет также функция Обозначим постоянную величину
х = xm cos ω0t. (3.14) Само же уравнение (3.11) принимает вид
График зависимости координаты тела от времени согласно (3.14) представляет собой косинусоиду (см. рис. 3.6). Период и частота гармонических колебанийПри колебаниях движения тела периодически повторяются. Промежуток времени Т, за который система совершает один полный цикл колебаний, называется периодом колебаний. Зная период, можно определить частоту колебаний, т. е. число колебаний в единицу времени, например за секунду. Если одно колебание совершается за время Т, то число колебаний за секунду
В Международной системе единиц (СИ) частота колебаний равна единице, если за секунду совершается одно колебание. Единица частоты называется герцем (сокращенно: Гц) в честь немецкого физика Г. Герца. Число колебаний за 2π с равно:
Величина ω0 — циклическая, или круговая, частота колебаний. Если в уравнении (3.14) время t равно одному периоду, то ω0Т = 2π. Таким образом, если в момент времени t = 0 х = хm, то и в момент времени t = Т х = хm, т. е. через промежуток времени, равный одному периоду, колебания повторяются. Частоту свободных колебаний называют собственной частотой колебательной системы1. 1 Часто в дальнейшем для краткости мы будем называть циклическую частоту просто частотой. Отличить циклическую частоту от обычной частоты можно по обозначениям.
|
|
|




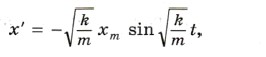
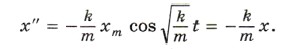
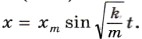
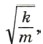 зависящую от свойств системы, через ω0:
зависящую от свойств системы, через ω0: