Главная >> Физика 11 кл. Мякишев

Глава 3. Механические колебания

§ 22. Гармонические колебания

Зная, как связаны между собой ускорение и координата колеблющегося тела, можно на основе математического анализа найти зависимость координаты от времени.

Ускорение

Ускорение — вторая производная координаты по времени. Мгновенная скорость точки, как вам известно из курса математики, представляет собой производную координаты точки по времени. Ускорение точки — это производная ее скорости по времени, или вторая производная координаты по времени. Поэтому уравнение (3.4) можно записать так:

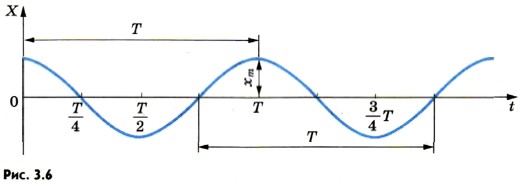
где х" — вторая производная координаты по времени. Согласно уравнению (3.11) при свободных колебаниях координата х изменяется со временем так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку.

Гармонические колебания

Из курса математики известно, что вторые производные синуса и косинуса по их аргументу пропорциональны самим функциям, взятым с противоположным знаком. В математическом анализе доказывается, что никакие другие функции таким свойством не обладают. Все это позволяет с полным основанием утверждать, что координата тела, совершающего свободные колебания, меняется с течением времени по закону синуса или косинуса. На рисунке 3.6 показано изменение координаты точки со временем по закону косинуса.

Периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса, называются гармоническими колебаниями.

Вначале мы будем рассматривать гармонические изменения координаты. В дальнейшем ознакомимся с гармоническими изменениями других величин.

Продолжение >>>