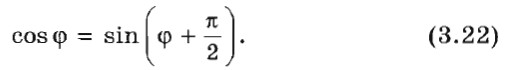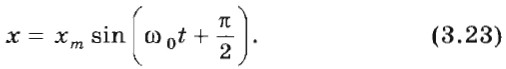|
|
|
|
|
Глава 3. Механические колебания
§ 23. Фаза колебанийВведем еще одну величину, характеризующую гармонические колебания, — фазу колебаний. При заданной амплитуде колебаний координата колеблющегося тела в любой момент времени однозначно определяется аргументом косинуса или синуса: φ = ω0t. Величину φ, стоящую под знаком функции косинуса или синуса, называют фазой колебаний, описываемой этой функцией. Выражается фаза в угловых единицах — радианах. Фаза определяет не только значение координаты, но и значение других физических величин, например скорости и ускорения, изменяющихся также по гармоническому закону. Поэтому можно сказать, что фаза определяет при заданной амплитуде состояние колебательной системы в любой момент времени. В этом состоит значение понятия фазы. Колебания с одинаковыми амплитудами и частотами могут различаться фазами. Так как
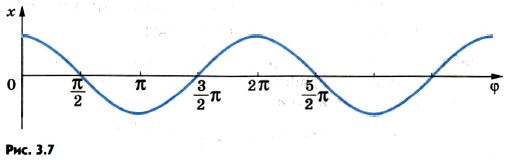
Отношение Можно изобразить на графике зависимость координаты колеблющейся точки не от времени, а от фазы. На рисунке 3.7 показана та же косинусоида, что и на рисунке 3.6, но на горизонтальной оси отложены вместо времени различные значения фазы φ. Представление гармонических колебаний с помощью косинуса и синусаВы уже знаете, что при гармонических колебаниях координата тела изменяется со временем по закону косинуса или синуса. После введения понятия фазы остановимся на этом подробнее.
Синус отличается от косинуса сдвигом аргумента на
Поэтому вместо формулы х = хm cos ω0t можно для описания гармонических колебаний использовать формулу
Но при этом начальная фаза, т. е. значение фазы в момент времени t = 0, равна не нулю, а
|
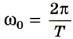, то
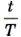указывает, сколько периодов прошло от момента начала колебаний. Любому значению времени t, выраженному в числе периодов Т, соответствует значение фазы φ, выраженное в радианах. Так, по прошествии времени 
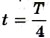(четверти периода) 
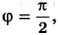по прошествии половины периода φ = π, по прошествии целого периода φ = 2π и т. д.
, что соответствует, как видно из уравнения (3.21), промежутку времени, равному четверти периода:
|
|