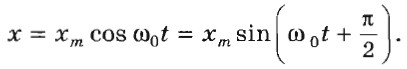Главная >> Физика 11 кл. Мякишев

Глава 3. Механические колебания

Фаза колебаний

Обычно колебания тела, прикрепленного к пружине, или колебания маятника мы возбуждаем, выводя тело маятника из положения равновесия и затем отпуская его. Смещение от положения равновесия максимально в начальной момент. Поэтому для описания колебаний удобнее пользоваться формулой (3.14) с применением косинуса, чем формулой (3.23) с применением синуса.

Но если бы мы возбудили колебания покоящегося тела кратковременным толчком, то координата тела в начальный момент была бы равна нулю, и изменения координаты со временем было бы удобнее описывать с помощью синуса, т. е. формулой

х = х_m sin ω₀t,                           (3.24)

так как при этом начальная фаза равна нулю.

Если в начальный момент времени (при t — 0) фаза колебаний равна φ, то уравнение колебаний можно записать в виде

х = х_m sin (ω₀t + φ).

Сдвиг фаз

Колебания, описываемые формулами (3.23) и (3.24), отличаются друг от друга только фазами. Разность фаз, или, как часто говорят, сдвиг фазу этих колебаний составляет . На рисунке 3.8 показаны графики зависимости координат от времени для двух гармонических колебаний, сдвинутых по фазе на . График 1 соответствует колебаниям, совершающимся по синусоидальному закону: х = х_m sin ω₀t, а график 2 — колебаниям, совершающимся по закону косинуса:

Для определения разности фаз двух колебаний надо в обоих случаях колеблющуюся величину выразить через одну и ту же тригонометрическую функцию — косинус или синус.

Вопросы к параграфу

1. Какие колебания называют гармоническими?

2. Как связаны ускорение и координата при гармонических колебаниях?

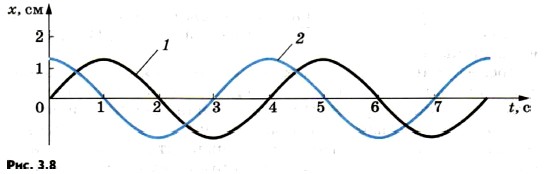
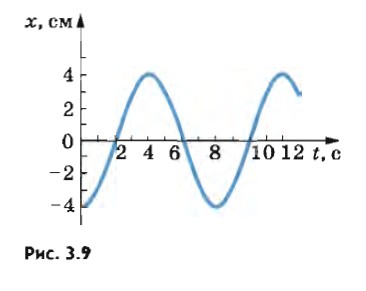
3. Как связаны циклическая частота колебаний и период колебаний?

4. Почему частота колебаний тела, прикрепленного к пружине, зависит от его массы, а частота колебаний математического маятника от массы не зависит?

5. Каковы амплитуды и периоды трех различных гармонических колебаний, графики которых представлены на рисунках 3.8, 3.9?

<<< К началу