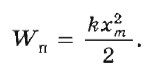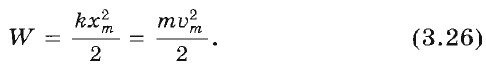|
|
|
|
|
Глава 3. Механические колебания § 24. Превращение энергии при гармонических колебанияхРассмотрим превращение энергии при гармонических колебаниях в двух случаях: в системе нет трения; в системе есть трение. Превращения энергии в системах без тренияСмещая шарик, прикрепленный к пружине (см. рис. 3.3), вправо на расстояние хm, мы сообщаем колебательной системе потенциальную энергию:
При движении шарика влево деформация пружины становится меньше, и потенциальная энергия системы уменьшается. Но одновременно увеличивается скорость и, следовательно, возрастает кинетическая энергия. В момент прохождения шариком положения равновесия потенциальная энергия колебательной системы становится равной нулю (Wп = 0 при х = 0). Кинетическая же энергия достигает максимума. После прохождения положения равновесия скорость шарика начинает уменьшаться. Следовательно, уменьшается и кинетическая энергия. Потенциальная же энергия системы снова увеличивается. В крайней левой точке она достигает максимума, а кинетическая энергия становится равной нулю. Таким образом, при колебаниях периодически происходит переход потенциальной энергии в кинетическую и обратно. Нетрудно проследить за тем, что такие же превращения механической энергии из одного ее вида в другой происходят и в случае математического маятника. Полная механическая энергия при колебаниях тела, прикрепленного к пружине, равна сумме кинетической и потенциальной энергий колебательной системы:
Кинетическая и потенциальная энергии периодически изменяются. Но полная механическая энергия изолированной системы, в которой отсутствуют силы сопротивления, сохраняется (согласно закону сохранения механической энергии) неизменной. Она равна либо потенциальной энергии в момент максимального отклонения от положения равновесия, либо же кинетической энергии в момент, когда тело проходит положение равновесия:
Энергия колеблющегося тела прямо пропорциональна квадрату амплитуды колебаний координаты или квадрату амплитуды колебаний скорости (см. формулу (3.26)).
|
|
|