|
|
|
|
|
§ 30. Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний Формула Томсона. Гармонические колебания заряда и токаФормула ТомсонаВ уравнении (3.11) коэффициент
Период свободных колебаний в контуре, таким образом, равен:
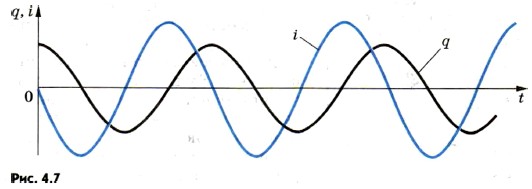
Формула (4.11) называется формулой Томсона в честь английского физика У. Томсона (Кельвина), который ее впервые вывел. Увеличение периода свободных колебаний с возрастанием L и С наглядно можно пояснить так. При увеличении индуктивности L ток медленнее нарастает со временем и медленнее падает до нуля. А чем больше емкость С, тем большее время требуется для перезарядки конденсатора. Гармонические колебания заряда и токаПодобно тому как координата при механических колебаниях (в случае, когда в начальный момент времени отклонение тела маятника от положения равновесия максимально) изменяется со временем по гармоническому закону: х = хm cos ω0t, заряд конденсатора меняется с течением времени по такому же закону: q = qm cos ω0t, (4.12) где qm — амплитуда колебаний заряда. Сила тока также совершает гармонические колебания:
где Im = qmω0 — амплитуда колебаний силы тока. Колебания силы тока опережают по фазе на
Точно так же колебания скорости тела в случае пружинного или математического маятника опережают на В действительности, из-за неизбежного наличия сопротивления электрической цепи, колебания будут затухающими. Сопротивление R также будет влиять и на период колебаний, чем больше сопротивление R, тем бо́льшим будет период колебаний. При достаточно большом сопротивлении колебания совсем не возникнут. Конденсатор разрядится, но перезарядки его не произойдет, энергия электрического и магнитного полей перейдет в тепло. Простейшая система, где наблюдаются свободные электромагнитные колебания, — колебательный контур. Уравнение (4.9) — это основное уравнение, описывающее свободные электрические колебания в контуре. Вопросы к параграфу 1. В чем различие между свободными и вынужденными электрическими колебаниями? 2. Как изменится период свободных электрических колебаний в контуре, если емкость конденсатора в нем вдвое увеличить или же вдвое уменьшить? 3. Как связаны амплитуды колебаний заряда и тока при разрядке конденсатора через катушку?
|
|
|



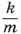 представляет собой квадрат собственной частоты колебаний. Поэтому и коэффициент
представляет собой квадрат собственной частоты колебаний. Поэтому и коэффициент 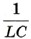 в уравнении (4.9) также представляет собой квадрат циклической частоты — в этот раз для свободных электрических колебаний:
в уравнении (4.9) также представляет собой квадрат циклической частоты — в этот раз для свободных электрических колебаний:


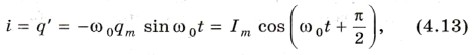
 колебания заряда (рис. 4.7).
колебания заряда (рис. 4.7).