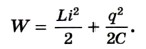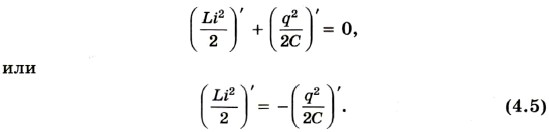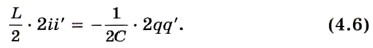Главная >> Физика 11 кл. Мякишев

Глава 4. Электромагнитные колебания

§ 30. Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний

Перейдем теперь к количественной теории процессов в колебательном контуре.

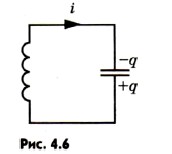
Уравнение, описывающее процессы в колебательном контуре. Рассмотрим колебательный контур, сопротивлением R которого можно пренебречь (рис. 4.6).

Уравнение, описывающее свободные электрические колебания в контуре, можно получить с помощью закона сохранения энергии. Полная электромагнитная энергия W контура в любой момент времени равна сумме его энергий магнитного и электрического полей:

Эта энергия не меняется с течением времени, если сопротивление R контура равно нулю. Значит, производная полной энергии по времени равна нулю. Следовательно, равна нулю сумма производных по времени от энергий магнитного и электрического полей:

Физический смысл уравнения (4.5) состоит в том, что скорость изменения энергии магнитного поля по модулю равна скорости изменения энергии электрического поля; знак «—» указывает на то, что, когда энергия электрического поля возрастает, энергия магнитного поля убывает (и наоборот).

Вычислив производные в уравнении (4.5), получим¹

¹ Мы вычисляем производные по времени. Поэтому производная (i²)' равна не просто 2i, как было бы при вычислении производной по i. Нужно 2i умножить еще на производную i' силы тока по времени, так как вычисляется производная от сложной функции. То же самое относится к производной (q²)'.

Но производная заряда по времени представляет собой силу тока в данный момент времени:

Поэтому уравнение (4.6) можно переписать в следующем виде:

Производная силы тока по времени есть не что иное, как вторая производная заряда по времени, подобно тому как производная скорости по времени (ускорение) есть вторая производная координаты по времени. Подставив в уравнение (4.8) i' = q" и разделив левую и правую части этого уравнения на Li, получим основное уравнение, описывающее свободные электрические колебания в контуре:

Теперь вы в полной мере можете оценить значение тех усилий, которые были затрачены для изучения колебаний шарика на пружине и математического маятника. Ведь уравнение (4.9) ничем, кроме обозначений, не отличается от уравнения (3.11), описывающего колебания шарика на пружине. При замене в уравнении (3.11) х на q, х" на q", k на 1/С и m на L мы в точности получим уравнение (4.9). Но уравнение (3.11) было уже решено выше. Поэтому, зная формулу, описывающую колебания пружинного маятника, мы сразу же можем записать формулу для описания электрических колебаний в контуре.

Окончание >>>