|
|
|
|
|
Глава 2. Механические колебания и волны Математический и пружинный маятникиСледует иметь также в виду, что проекция скорости маятника на ось X имеет разные знаки в зависимости от направления движения. При движении от точки А к точке О проекция скорости на эту ось отрицательна, а при движении от точки В к точке О — положительна. То же относится к проекциям силы F и ускорения на ось X: при движении от точки О к точке А они отрицательны, а при движении от точки О к точке В — положительны. 4. Пользуясь вторым законом Ньютона
Отсюда
Поскольку проекция ускорения и проекция смещения направлены в противоположные стороны, получаем
т. е. сила, действующая в колебательной системе, прямо пропорциональна смещению и направлена в противоположную сторону и соответственно ускорение колебаний математического маятника прямо пропорционально его смещению. 5. Рассмотрим ещё одну колебательную систему — пружинный маятник.
В этой модели маятника мы пренебрегаем массой пружины по сравнению с массой груза, деформацией тела по сравнению с деформацией пружины. Кроме того, считаем, что деформация пружины подчиняется закону Гука: Fупр = -kx. Рассмотрим движение такого маятника 6. Пока пружина не деформирована (рис. 80, а) (точка О), груз находится в положении равновесия. При этом на груз в горизонтальном направлении силы не действуют.
6. Пока пружина не деформирована (рис. 80, а) (точка О), груз находится в положении равновесия. При этом на груз в горизонтальном направлении силы не действуют. Выведем груз из положения равновесия, растянув пружину (рис. 80, б), и отпустим его (точка A). На груз будет действовать сила упругости пружины
|
|
|



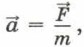 запишем уравнение колебаний математического маятника. Для этого, используя рисунок 79, выразим силу F. При малых смещениях треугольники АОС и ADE подобны, как треугольники с общим углом и со взаимно параллельными сторонами. Соответственно
запишем уравнение колебаний математического маятника. Для этого, используя рисунок 79, выразим силу F. При малых смещениях треугольники АОС и ADE подобны, как треугольники с общим углом и со взаимно параллельными сторонами. Соответственно
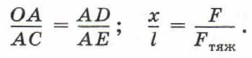
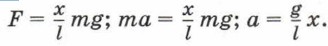
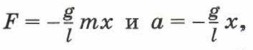
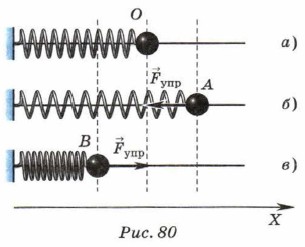
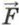 упр, пропорциональная её удлинению и направленная к положению равновесия. Под действием этой силы груз начнёт двигаться к положению равновесия. Вследствие инертности он пройдёт положение равновесия. Пружина сожмётся, и в ней опять возникнет сила упругости. Дойдя до крайнего левого положения (точка В), груз остановится, а затем под действием силы упругости начнёт двигаться к положению равновесия (рис. 80, в). Пройдя его, он отклонится вправо, и процесс повторится.
упр, пропорциональная её удлинению и направленная к положению равновесия. Под действием этой силы груз начнёт двигаться к положению равновесия. Вследствие инертности он пройдёт положение равновесия. Пружина сожмётся, и в ней опять возникнет сила упругости. Дойдя до крайнего левого положения (точка В), груз остановится, а затем под действием силы упругости начнёт двигаться к положению равновесия (рис. 80, в). Пройдя его, он отклонится вправо, и процесс повторится.