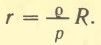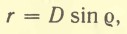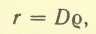|
|
|
|
|
12. Определение расстояний и размеров тел в Солнечной системе Определение размеров светил
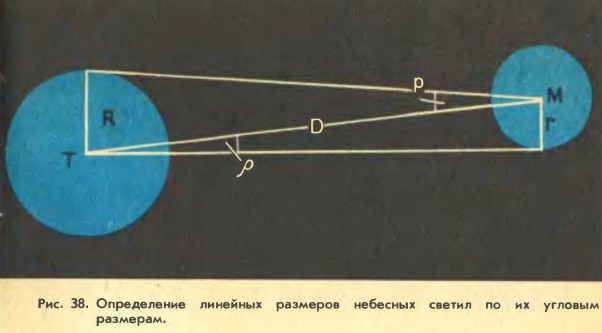
На рисунке 38 T — центр Земли, М — центр светила линейного радиуса r. По определению горизонтального параллакса радиус Земли R виден со светила под углом р. Радиус же светила r виден с Земли под углом
то ясно, что
Если углы
Этот способ определения размеров светил применим только тогда, когда виден диск светила. Зная расстояние D до светила и измерив его угловой радиус
или
если угол Расстояния до очень далеких светил узнают не по параллаксу, а иными способами. Вопросы 1. Во сколько раз Солнце больше, чем Луна, если их угловые диаметры одинаковы, а горизонтальные параллаксы соответственно равны 8,8" и 57'? 2. Чему равен угловой диаметр Солнца, видимого с Плутона? 3. Чему равен линейный диаметр Луны, если она видна с расстояния 400 000 км под углом примерно 0,5°? 4. Во сколько раз больше получает энергии от Солнца каждый квадратный метр поверхности Меркурия, чем Марса? Нужные данные возьмите из приложений. 5. В каких точках небосвода земной наблюдатель видит светило, находясь в точках В и А (рис. 37)? 6. В каком отношении численно меняется видимый с Земли и с Марса угловой диаметр Солнца от перигелия к афелию, если эксцентриситеты их орбит соответственно равны 0,017 и 0,093.
|
|
|



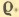 Поскольку
Поскольку
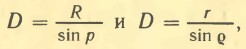
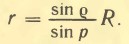
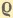 и р малы, то синусы пропорциональны углам и можно написать:
и р малы, то синусы пропорциональны углам и можно написать: