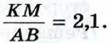|
|
§ 1. Определение подобных треугольников



Задачи к § 1. Определение подобных треугольников
533.  Найдите отношение отрезков АВ и CD, если их длины равны соответственно 15 см и 20 см. Изменится ли это отношение, если длины отрезков выразить в миллиметрах? Найдите отношение отрезков АВ и CD, если их длины равны соответственно 15 см и 20 см. Изменится ли это отношение, если длины отрезков выразить в миллиметрах?
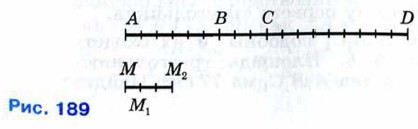
534. Пропорциональны ли изображённые на рисунке 189 отрезки: а) АС, CD и М1М2, ММ1; б) АВ, ВС, CD и ММ2, ММ1, М1М2; в) АВ, BD и ММ1, М1М2?
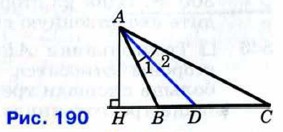
535. Докажите, что биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
Решение
Пусть AD — биссектриса треугольника АВС. Докажем, что 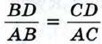 (рис. 190). Треугольники ABD и ACD имеют общую высоту АН, поэтому (рис. 190). Треугольники ABD и ACD имеют общую высоту АН, поэтому 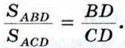 С другой стороны, эти же треугольники имеют по равному углу (∠1 = ∠2), поэтому С другой стороны, эти же треугольники имеют по равному углу (∠1 = ∠2), поэтому 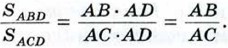 Из двух равенств для отношения площадеи получаем Из двух равенств для отношения площадеи получаем 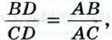 или или 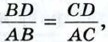 что и требовалось доказать. что и требовалось доказать.
536.  Отрезок BD является биссектрисой треугольника АВС. Отрезок BD является биссектрисой треугольника АВС.
а) Найдите АВ, если ВС = 9 см, АО = 7,5 см, ОС = 4,5 см.
б) Найдите ОС, если АВ = 30, АО = 20, ВС =16.
537.  Отрезок АО является биссектрисой треугольника АВС. Найдите ВО и ОС, если АВ = 14 см, ВС = 20 см, АС = 21 см. Отрезок АО является биссектрисой треугольника АВС. Найдите ВО и ОС, если АВ = 14 см, ВС = 20 см, АС = 21 см.
538.  Биссектриса АО треугольника АВС делит сторону ВС на отрезки СО и ВО, равные соответственно 4,5 см и 13,5 см. Найдите АВ и АС, если периметр треугольника АВС равен 42 см. Биссектриса АО треугольника АВС делит сторону ВС на отрезки СО и ВО, равные соответственно 4,5 см и 13,5 см. Найдите АВ и АС, если периметр треугольника АВС равен 42 см.
539.  В треугольник MNK вписан ромб MDEF так, что вершины D, Е и F лежат соответственно на сторонах MN, NK и МК. Найдите отрезки NE и ЕК, если MN = 7 см, NK = 6 см, МК = 5 см. В треугольник MNK вписан ромб MDEF так, что вершины D, Е и F лежат соответственно на сторонах MN, NK и МК. Найдите отрезки NE и ЕК, если MN = 7 см, NK = 6 см, МК = 5 см.
540. Периметр треугольника CDE равен 55 см. В этот треугольник вписан ромб DMFN так, что вершины М, F и N лежат соответственно на сторонах СО, СЕ и DE. Найдите стороны СО и DE, если CF = 8 см, EF = 12 см.
541. Подобны ли треугольники АВС и DEF, если ∠A = 106°, ∠B = 34°, ∠B =106°, ∠B = 40°, АС = 4,4 см, АВ = 5,2 см, ВС = = 7,6 см, DE = 15,6 см, DF = 22,8 см, EF = 13,2 см?
542.  В подобных треугольниках АВС и KMN стороны АВ и КМ, ВС и MN являются сходственными. Найдите стороны треугольника KMN, если АВ = 4 см, ВС = 5 см, СА = 7 см, В подобных треугольниках АВС и KMN стороны АВ и КМ, ВС и MN являются сходственными. Найдите стороны треугольника KMN, если АВ = 4 см, ВС = 5 см, СА = 7 см, 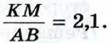
Окончание >>>
|



 Найдите отношение отрезков АВ и CD, если их длины равны соответственно 15 см и 20 см. Изменится ли это отношение, если длины отрезков выразить в миллиметрах?
Найдите отношение отрезков АВ и CD, если их длины равны соответственно 15 см и 20 см. Изменится ли это отношение, если длины отрезков выразить в миллиметрах?
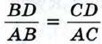 (рис. 190). Треугольники ABD и ACD имеют общую высоту АН, поэтому
(рис. 190). Треугольники ABD и ACD имеют общую высоту АН, поэтому 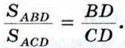 С другой стороны, эти же треугольники имеют по равному углу (∠1 = ∠2), поэтому
С другой стороны, эти же треугольники имеют по равному углу (∠1 = ∠2), поэтому 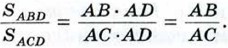 Из двух равенств для отношения площадеи получаем
Из двух равенств для отношения площадеи получаем 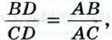 или
или 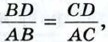 что и требовалось доказать.
что и требовалось доказать.