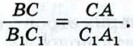|
|
|
|
|
§ 2. Признаки подобия треугольников Первый признак подобия треугольниковТеорема
Доказательство Пусть
По теореме о сумме углов треугольника ∠C = 180° - ∠A - ∠B, ∠C1 = 180° - ∠A1 - ∠B1, и, значит, ∠C = ∠C1. Таким образом, углы треугольника АВС соответственно равны углам треугольника А1В1С1. Докажем, что стороны треугольника АВС пропорциональны сходственным сторонам треугольника А1В1С1. Так как ∠A = ∠A1 и ∠C = ∠C1, то Из этих равенств следует, что Итак, стороны треугольника АВС пропорциональны сходственным сторонам треугольника А1В1С1. Теорема доказана.
|
|
|



 АВС и
АВС и 
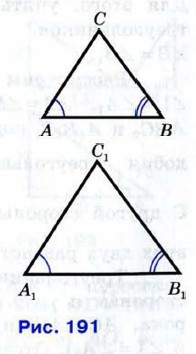
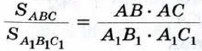 и
и 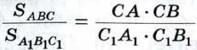 (см. п. 53).
(см. п. 53).
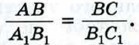 Аналогично, используя равенства ∠A = ∠A1, ∠B = ∠B1, получаем
Аналогично, используя равенства ∠A = ∠A1, ∠B = ∠B1, получаем