|
|
|
|
|
§ 3. Умножение вектора на число. Применение векторов к решению задач Задачи к § 3. Умножение вектора на число779. 780. Докажите, что для любого вектора 780. 781. 782. 783.
784. Точки М и N — середины диагоналей АС и BD четырёхугольника ABCD. Докажите, что
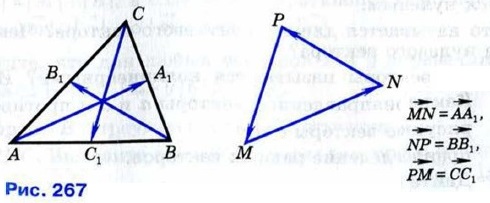
786. 787. Применение векторов к решению задач788. Дан произвольный треугольник АВС. Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника АВС. Решение Пусть АА1, ВВ1, СС1 — медианы треугольника АВС. Тогда
Отсюда следует, что если мы построим сумму векторов
789. На сторонах треугольника АВС построены параллелограммы АВВ1А2, ВСС1В2, АСС2А1. Докажите, что существует треугольник, стороны которого соответственно параллельны и равны отрезкам А1А2, В1В2 и С1С2. 790. Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен её основаниям и равен полуразности оснований. 791. Докажите, что отрезки, соединяющие середины противоположных сторон произвольного четырёхугольника, точкой пересечения делятся пополам. 792. Докажите теорему о средней линии треугольника (п. 64).
|
|
|



 Дан вектор
Дан вектор 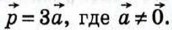 Как направлен каждый из векторов
Как направлен каждый из векторов 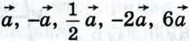 по отношению к вектору
по отношению к вектору 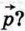 Выразите длины этих векторов через
Выразите длины этих векторов через 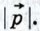
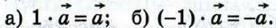
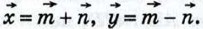 Выразите через
Выразите через 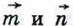 векторы:
векторы: 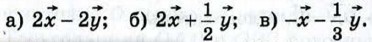
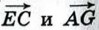 через векторы
через векторы 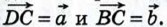
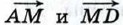 через векторы
через векторы 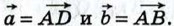
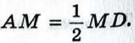 Выразите через векторы
Выразите через векторы 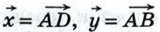 следующие векторы:
следующие векторы:
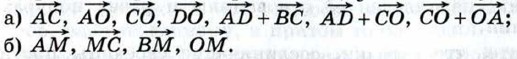
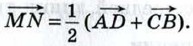
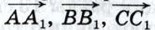 через векторы
через векторы 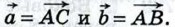
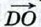 через векторы
через векторы 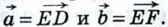
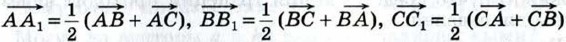 (см. задачу 1, п. 87). Сложив эти равенства, получим
(см. задачу 1, п. 87). Сложив эти равенства, получим
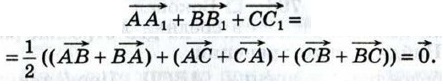
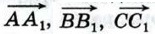 по правилу многоугольника (п. 84), то получим треугольник, удовлетворяющий условиям задачи (треугольник MNP на рисунке 267).
по правилу многоугольника (п. 84), то получим треугольник, удовлетворяющий условиям задачи (треугольник MNP на рисунке 267).