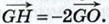|
|
|
|
|
Глава VIII. Окружность Ответы к задачам повышенной трудности: Глава IX. Векторы904. Параллелограмм. 905. Параллелограмм. Указание. Воспользоваться задачей 1, п. 87. 906. Указание. Учесть, что длины векторов 907. Указание. Пусть точки A, В и С лежат на одной прямой. Сначала доказать, что в этом случае 908. Указание. Пусть в четырёхугольнике ABCD точки Е и F — середины диагоналей АС и BD, a G — точка пересечения отрезков, соединяющих середины противоположных сторон. Используя задачу 791, для произвольной точки О выразить векторы 909. Указание. Воспользоваться задачами 619 и 907. 910. Указание. Пусть A1, В1 и С1 — середины сторон ВС, СА и АВ треугольника АВС. Пользуясь тем, что
|
|
|



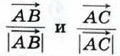 равны.
равны.
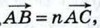 где n — некоторое число. В качестве k, l, m можно взять, например, числа k = n - 1, l = 1, m = -n. При доказательстве обратного утверждения взять точку О, совпадающую с точкой А.
где n — некоторое число. В качестве k, l, m можно взять, например, числа k = n - 1, l = 1, m = -n. При доказательстве обратного утверждения взять точку О, совпадающую с точкой А.
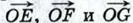 через
через 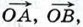
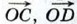 и воспользоваться задачей 907.
и воспользоваться задачей 907.
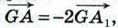
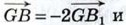
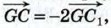 доказать, что
доказать, что