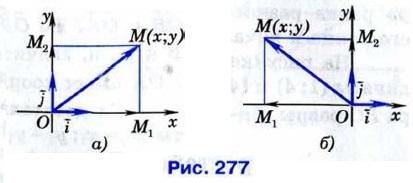
Связь между координатами вектора и координатами его начала и конца

Рассмотрим прямоугольную систему координат и какую-нибудь точку М с координатами (x; у). Напомним, как определяются числа х и у. Проведём через точку М прямые, перпендикулярные к осям координат, и обозначим через М₁ и М₂ точки пересечения этих прямых с осями Ох и Оу (рис. 277). Число х (абсцисса точки М) определяется так: х = ОМ₁, если М₁ — точка положительной полуоси (рис. 277, а), х = -ОМ₁, если М₁ — точка отрицательной полуоси (рис. 277, б); x = 0, если М, совпадает с точкой О.

Рис. 227

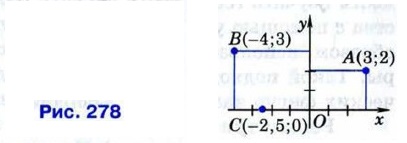
Аналогично определяется число у (ордината точки М). На рисунке 278 изображена прямоугольная система координат Оху и отмечены точки А (3; 2), В (-4; 3), С (-2,5; 0).

Рис. 228

Вектор назовём радиус-вектором точки М. Докажем, что координаты точки М равны соответствующим координатам её радиус-вектора. Воспользуемся равенством 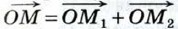(см. рис. 277) и докажем, что 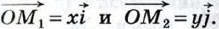Если x > 0 (как на рисунке 277, а), то х = ОМ₁, а векторы 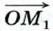и 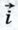сонаправлены. Поэтому 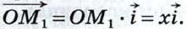Если х < 0 (как на рисунке 277,6), то 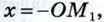а векторы 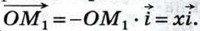и противоположно направлены. Поэтому Наконец, если х = 0, то 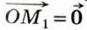и равенство 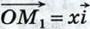в этом случае также справедливо. Таким образом, в любом случае 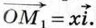Аналогично доказывается, что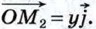

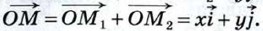Следовательно, Отсюда следует, что координаты радиус-вектора 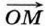равны {ж; у), т. е. равны соответствующим координатам точки М, что и требовалось доказать.

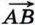Пользуясь доказанным утверждением, выразим координаты вектора через координаты его начала А и конца В. Пусть точка А имеет координаты (x₁; y₁), а точка В — координаты (x₂; у₂). Вектор 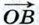равен разности векторов и 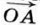(рис. 279), поэтому его координаты равны Разностям соответствующих координат векторов 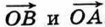. Но радиус-векторы точек В и А, и, значит, имеет координаты {х₂; y₂}, а имеет координаты {х₁; y₁}.

Следовательно, вектор имеет координаты {x₂ - x₁, у₂ - у₁}.

Таким образом, каждая координата вектора равна разности соответствующих координат его конца и начала.

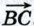На рисунке 275 точки В и С имеют координаты (1; 4) и (4; 2), поэтому координаты вектора равны {3; -2}.