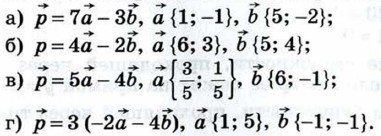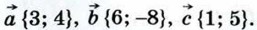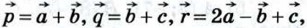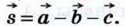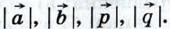|
|
|
|
|
Глава X. Метод координат Дополнительные задачи к главе X. Метод координат988. Векторы
989. Найдите координаты вектора
990. Даны векторы а) Найдите координаты векторов б) Найдите 991. Докажите, что расстояние между любыми двумя точками М1 (x1; 0) и М2 (х2; 0) оси абсцисс вычисляется по формуле d = |х1 - х2|. 992. Докажите, что треугольник АВС, вершины которого имеадт координаты А (4; 8), В (12; 11), С (7; 0), является равнобедренным, но не равносторонним. 993. Докажите, что углы А и С треугольника АВС равны, если А (-5; 6), В (3; -9) и С (-12; -17). 994. Докажите, что точка D равноудалена от точек А, В и С, если: а) D (1; 1), А (5; 4), В (4; -3), С (-2; 5);
995. На оси абсцисс найдите точку, равноудалённую от точек М, (-2; 4) и М2 (6; 8). 996. Вершины треугольника АВС имеют координаты А (-5; 13), В (3; 5), С(-3;-1). Найдите: а) координаты середин сторон треугольника; б) медиану, проведённую к стороне АС; в) средние линии треугольника. 997. Докажите, что четырёхугольник ABCD, вершины которого имеют координаты А (3; 2), В (0; 5), С (-3; 2), D (0; -1), является квадратом. 998. Докажите, что четырёхугольник ABCD, вершины которого имеют координаты А (-2;-3), 13 (1; 4), С (8; 7), D (5; 0), является ромбом. Найдите его площадь. 999. Найдите координаты четвёртой вершины параллелограмма по заданным координатам трёх его вершин: (-4; 4), (-5; 1) и (-1; 5). Сколько решений имеет задача?
|
|
|



 и
и  не коллинеарны. Найдите такое число х (если это возможно), чтобы векторы
не коллинеарны. Найдите такое число х (если это возможно), чтобы векторы 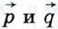 были коллинеарны:
были коллинеарны:
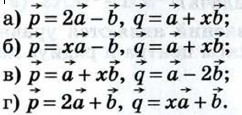
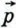 и его длину, если:
и его длину, если: