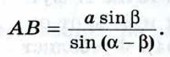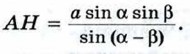|
|
|
|
|
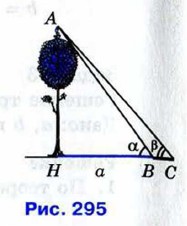
§ 2. Соотношения между сторонами и углами треугольника Измерительные работыТригонометрические формулы используются при проведении различных измерительных работ на местности. Измерение высоты предмета.Предположим, что требуется определить высоту АН какого-то предмета (рис. 295). Для этого отметим точку В на определённом расстоянии а от основания Н предмета и измерим угол ABH: ∠ABH = α. По этим данным из прямоугольного треугольника АНВ находим высоту предмета: АН = a tg α.
Если основание предмета недоступно, то можно поступить так: на прямой, проходящей через основание Н предмета, отметим две точки B и С на определённом расстоянии а друг от друга и измерим углы АВН и АСВ: ∠ABH= α. и ∠ACB = β (см. рис. 295). Эти данные позволяют определить все элементы треугольника АВС, в частности АВ. В самом деле, ∠ABH — внешний угол треугольника АВС, поэтому ∠A = α - β. Используя теорему синусов, находим АВ:
Из прямоугольного треугольника АВН находим высоту АН предмета: АН = АВ • sin α. Итак,
|
|
|