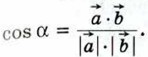|
§ 3. Скалярное произведение векторов



Скалярное произведение в координатах
Скалярное произведение двух векторов можно вычислить, зная координаты этих векторов.
Теорема
| В прямоугольной системе координат скалярное произведение векторов α {x1; y1) и β {х2; у2} выражается формулой
|
Доказательство
Если хотя бы один из векторов  и и  нулевой, то справедливость равенства (2) очевидна, так как координаты нулевого вектора равны нулю. Рассмотрим случай, когда векторы нулевой, то справедливость равенства (2) очевидна, так как координаты нулевого вектора равны нулю. Рассмотрим случай, когда векторы  и и  ненулевые. Отложим от произвольной точки О векторы ненулевые. Отложим от произвольной точки О векторы 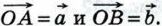 Если векторы Если векторы  и и  не коллинеарны (рис. 304, а), то по теореме косинусов не коллинеарны (рис. 304, а), то по теореме косинусов
Это равенство верно и в том случае, когда векторы  и и  коллинеарны (рис. 304, б, в). коллинеарны (рис. 304, б, в).
Так как 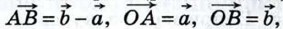 то равенство (3) можно записать так: то равенство (3) можно записать так: 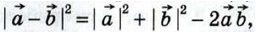
Векторы  , ,  и и  - -  имеют координаты {x1; y1}, {х2; у2} и {х2 - х1; у2 - у1}, поэтому имеют координаты {x1; y1}, {х2; у2} и {х2 - х1; у2 - у1}, поэтому
Подставив эти выражения в правую часть равенства (4), после несложных преобразований получим формулу (2). Теорема доказана.
Следствие 1
Ненулевые векторы  {x1; y1} и {x1; y1} и  {х2; у2} перпендикулярны тогда и только тогда, когда x1x2 + y1y2 = 0. {х2; у2} перпендикулярны тогда и только тогда, когда x1x2 + y1y2 = 0.
|
Следствие 2
Косинус угла α между ненулевыми векторами  {х1; у1} и {х1; у1} и  {х2; у2} выражается формулой {х2; у2} выражается формулой
|
В самом деле, так как 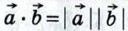 cos α, то cos α, то 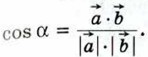
Подставив сюда выражения для  • •  | | | и | | и | | через координаты векторов | через координаты векторов  и и  получим формулу (5). получим формулу (5).
| 


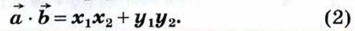
 и
и  нулевой, то справедливость равенства (2) очевидна, так как координаты нулевого вектора равны нулю. Рассмотрим случай, когда векторы
нулевой, то справедливость равенства (2) очевидна, так как координаты нулевого вектора равны нулю. Рассмотрим случай, когда векторы 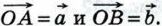 Если векторы
Если векторы 
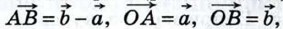 то равенство (3) можно записать так:
то равенство (3) можно записать так: 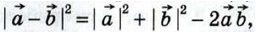
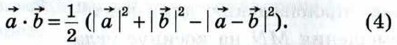
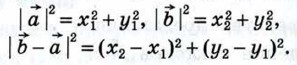
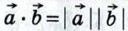 cos α, то
cos α, то