Главная >> Геометрия 7—9 классы. Атанасян

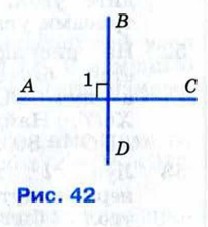
§ 6. Перпендикулярные прямые

Перпендикулярные прямые

Рассмотрим две пересекающиеся прямые (рис. 42). Они образуют четыре неразвёрнутых угла. Если один из них прямой (угол 1), то остальные углы также прямые (объясните почему).

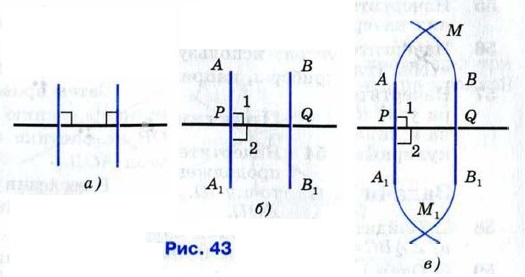
Две пересекающиеся прямые называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла.

Перпендикулярность прямых АС и BD обозначается так: AC⊥BD (читается: «Прямая АС перпендикулярна к прямой BD»).

Отметим, что две прямые, перпендикулярные к третьей, не пересекаются (рис. 43, а).

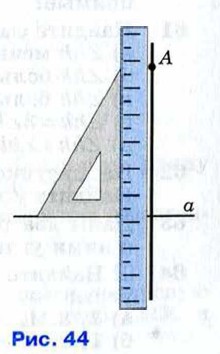
В самом деле, рассмотрим прямые АА₁ и ВВ₁, перпендикулярные к прямой PQ (рис. 43, б). Мысленно перегнём рисунок по прямой PQ так, чтобы верхняя часть рисунка наложилась на нижнюю. Так как прямые углы 1 и 2 равны, то луч РА наложится на луч РА₁. Аналогично, луч QB наложится на луч QB₁.

Поэтому, если предположить, что прямые АА₁ и ВВ₁ пересекаются в точке М, то эта точка наложится на некоторую точку М₁, также лежащую на этих прямых (рис. 43, в), и мы получим, что через точки М и М₁ проходят две прямые: А А₁ и ВВ₁. Но это невозможно.

Следовательно, наше предположение неверно и, значит, прямые АА₁ и ВВ₁ не пересекаются.

Для проведения перпендикулярных прямых используют чертёжный угольник и линейку (рис. 44).