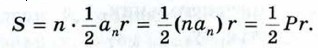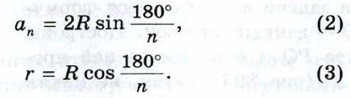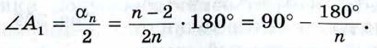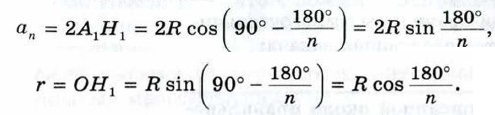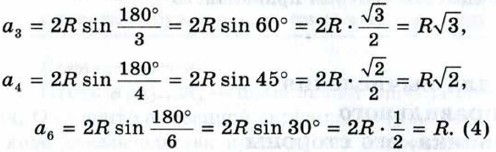|
|
|
|
|
§ 1. Правильные многоугольники Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружностиПусть S — площадь правильного n-угольника, аn — его сторона, Р — периметр, а r и R — радиусы соответственно вписанной и описанной окружностей. Докажем сначала, что
Соединим центр данного многоугольника с его вершинами (см. рис. 308). Тогда многоугольник разобьётся на n равных треугольников, площадь каждого из которых будет равна
Выведем далее формулы:
Для вывода этих формул воспользуемся рисунком 308. В прямоугольном треугольнике А1Н1О
Следовательно,
Полагая в формуле (2) n = 3, 4 и 6, получим выражения для сторон правильного треугольника, квадрата и правильного шестиугольника:
|
|
|




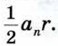 Следовательно,
Следовательно,