|
|
|
|
|
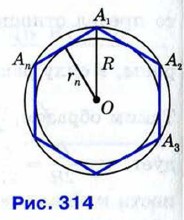
§ 2. Длина окружности и площадь круга Площадь кругаНапомним, что кругом называется часть плоскости, ограниченная окружностью. Круг радиуса R с центром О содержит точку О и все точки плоскости, находящиеся от точки О на расстоянии, не большем R. Выведем формулу для вычисления площади круга радиуса R. Для этого рассмотрим правильный n-угольник А1А2...Аn, вписанный в окружность, ограничивающую круг (рис. 314). Очевидно, площадь S данного круга больше площади Sn многоугольника А1А2...Аn, так как этот многоугольник целиком содержится в данном круге. С другой стороны, площадь S'n, круга, вписанного в многоугольник, меньше Sn, так как этот круг целиком содержится в многоугольнике. Итак, S'n < Sn < S. (2)
Будем теперь неограниченно увеличивать число сторон многоугольника. По формуле (3) § 1 имеем По формуле (1) § 1 S = πR2. Замечание В течение веков усилия многих математиков были направлены на решение задачи, получившей название задача о квадратуре круга: построить при помощи циркуля и линейки квадрат, площадь которого равна площади данного круга. Только в конце XIX века было доказано, что такое построение невозможно.
|
|
|



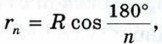 где rn — радиус вписанной в многоугольник окружности. При n → ∞
где rn — радиус вписанной в многоугольник окружности. При n → ∞ 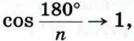 поэтому rn → R. Иными словами, при неограниченном увеличении числа сторон многоугольника вписанная в него окружность «стремится» к описанной окружности, поэтому S'n → 5 при n → ∞. Отсюда и из неравенств (2) следует, что Sn → S при n → ∞.
поэтому rn → R. Иными словами, при неограниченном увеличении числа сторон многоугольника вписанная в него окружность «стремится» к описанной окружности, поэтому S'n → 5 при n → ∞. Отсюда и из неравенств (2) следует, что Sn → S при n → ∞.
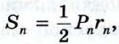 где Рn — периметр многоугольника А1А2...Аn. Учитывая, что rn → R, Рn → 2πR, Sn → S при n → ∞, получаем
где Рn — периметр многоугольника А1А2...Аn. Учитывая, что rn → R, Рn → 2πR, Sn → S при n → ∞, получаем 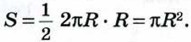 Итак, для вычисления площади S круга радиуса R мы получили формулу
Итак, для вычисления площади S круга радиуса R мы получили формулу