|
|
|
|
|
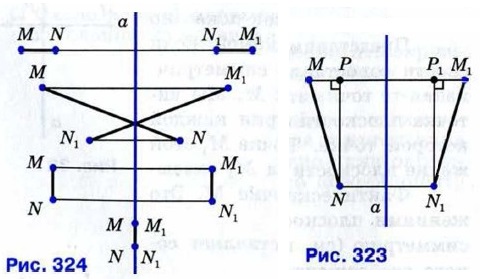
§ 1. Понятие движения Понятие движенияОсевая симметрия обладает следующим важным свойством — это отображение плоскости на себя, которое сохраняет расстояния между точками. Поясним, что это значит. Пусть М и N — какие-либо точки, а М1 и N1 — симметричные им точки относительно прямой а (рис. 323). Из точек N и N1 проведём перпендикуляры NP и N1P1 к прямой ММ1. Прямоугольные треугольники MNP и M1N1P1 равны по двум катетам: МР = М1Р1 и NP = N1P1 (объясните, почему эти катеты равны). Поэтому гипотенузы MN и M1N1 также равны. Следовательно, расстояние между точками М и N равно расстоянию между симметричными им точками М1 и N1. Другие случаи расположения точек М, N и М1, N1 рассмотрите самостоятельно и убедитесь в том, что и в этих случаях MN = M1N1 (рис. 324). Таким образом, осевая симметрия является отображением, которое сохраняет расстояния между точками. Любое отображение, обладающее этим свойством, называется движением (или перемещением).
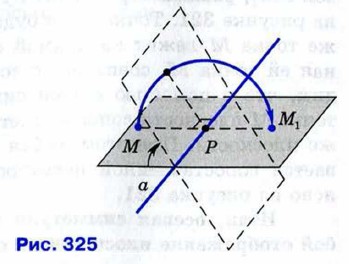
Итак, движение плоскости — это отображение плоскости на себя, сохраняющее расстояния. Почему отображение, сохраняющее расстояния, называют движением (или перемещением), можно пояснить на примере осевой симметрии. Её можно представить как поворот плоскости в пространстве на 180° вокруг оси а. На рисунке 325 показано, каким образом происходит такой поворот.
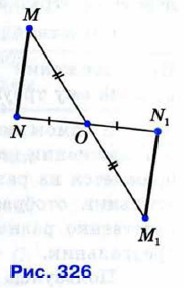
Отметим, что центральная симметрия плоскости также является движением (пользуясь рисунком 326, убедитесь в этом самостоятельно).
|
|
|