|
|
|
|
|
§ 1. Многогранники ПараллелепипедЧетырёхугольная призма, основаниями которой являются параллелограммы, называется параллелепипедом (рис. 345). Все шесть граней параллелепипеда — параллелограммы.
Если параллелепипед прямой, т. е. его боковые рёбра перпендикулярны к плоскостям оснований, то боковые грани — прямоугольники. Если же и основаниями прямого параллелепипеда служат прямоугольники, то этот параллелепипед — прямоугольный. Мы знаем, что диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. Оказывается, что аналогичным свойством обладают диагонали параллелепипеда:
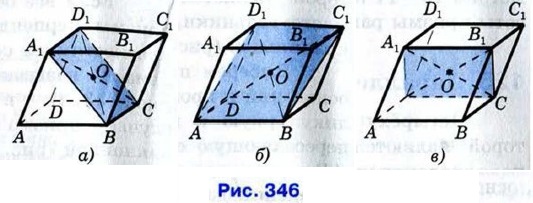
Доказательство этого утверждения основано на следующем факте: если две прямые в пространстве параллельны третьей прямой, то они параллельны. В том случае, когда все три прямые лежат в одной плоскости, это утверждение было доказано в п. 28. В общем случае оно будет доказано в курсе стереометрии 10—11 классов. Обратимся к рисунку 346, а, на котором изображён параллелепипед ABCDA1B1C1D1. Поскольку грани ABCD и ADD1A1 — параллелограммы, то BC || AD, BC = AD, A1D1 || AD, A1D1 = AD. Из этого следует, что BC = A1D1 и ВС || A1D1, поэтому четырёхугольник A1D1CB — параллелограмм, а значит, его диагонали А1С и D1B, являющиеся также диагоналями параллелепипеда, пересекаются в некоторой точке О и делятся этой точкой пополам.
Аналогично доказывается, что четырёхугольник AD1C1B — параллелограмм (рис. 346, б), и, следовательно, его диагонали АС1 и D1B пересекаются и точкой пересечения делятся пополам. Но серединой диагонали D1B является точка О. Таким образом, диагонали А1С, D1B и АС1 параллелепипеда пересекаются в точке О и делятся этой точкой пополам. Наконец, рассматривая четырёхугольник A1B1CD (рис. 346, в), точно так же устанавливаем, что и четвёртая диагональ DB1 проходит через точку О и делится ею пополам.
|
|
|