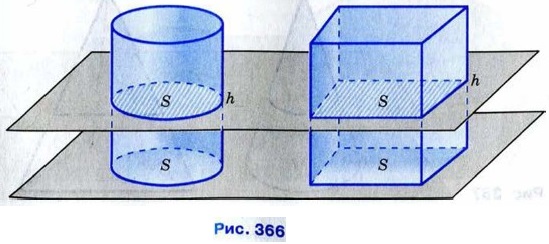
Задачи к § 2. Тела и поверхности вращения

1213. Докажите, что объём цилиндра равен произведению площади основания на высоту.

Решение

Воспользуемся принципом Кавальери. Рассмотрим цилиндр и призму с площадями оснований, равными S, и высотами, равными h, «стоящие» на одной плоскости (рис. 366). Любая секущая плоскость, параллельная этой плоскости, даёт в качестве сечения цилиндра круг площади S, а в качестве сечения призмы — многоугольник площади S. Значит, объём цилиндра равен объёму призмы. Но объём призмы равен Sh. Поэтому и объём цилиндра равен Sh.

Рис. 366

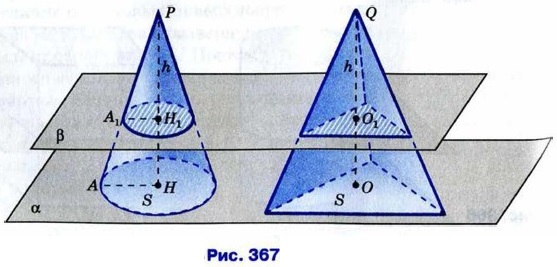
1214. Пусть V, r и h — соответственно объём, радиус и высота цилиндра. Найдите: а) V, если u = 2√2 см, h = 3 см; б) r, если V = 120cм³, h = 3,6 см; в) h, если r = h, V = 8π см³.

1215. В цилиндр вписана правильная п-угольная призма (т. е. основания призмы вписаны в основания цилиндра). Найдите отношение объёмов призмы и цилиндра, если: а) n = 3; б) n = 4; в) n = 6; г) n = 8; д) n — произвольное натуральное число.

1216. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длине окружности основания. Найдите площадь боковой поверхности цилиндра.

1217. Сколько квадратных метров листовой жести пойдёт на изготовление трубы длиной 4 м и диаметром 20 см, если на швы необходимо добавить 2,5% площади её боковой поверхности?

1218. Один цилиндр получен вращением прямоугольника ABCD вокруг прямой АВ, а другой цилиндр — вращением этого же прямоугольника вокруг прямой ВС. а) Докажите, что площади боковых поверхностей этих цилиндров равны, б) Найдите отношение площадей полных поверхностей этих цилиндров, если АВ = а, ВС = b.

1219.*Докажите, что объём конуса равен одной трети произведения площади основания на высоту.

Решение

Воспользуемся принципом Кавальери. Рассмотрим конус и пирамиду с площадями оснований S и высотами PH = h и QO = h соответственно, «стоящие» на одной плоскости α (рис. 367). Докажем, что объём конуса равен

Рис. 367

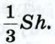
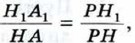Проведём секущую плоскость β, параллельную плоскости а и пересекающую высоты PH и QO в точках Н₁ и O₁ соответственно. В сечении конуса плоскостью β получится круг радиуса Н₁А₁. Треугольники РН₁А₁₁и PHА подобны по двум углам (∠P — общий, ∠PH₁А₁ = ∠PHA = 90°, так как в противном случае прямые НА и Н₁А₁, а значит, и плоскости α и β пересекались бы, что противоречит условию). Поэтому откуда 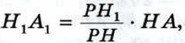и площадь сечения конуса равна

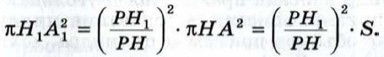
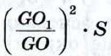Площадь сечения пирамиды равна (см. задачу 1209). По условию PH = QO = h. Интуитивно ясно также, что РН₁ = QO₁ (аккуратное доказательство этого факта будет дано в курсе стереометрии 10—11 классов).

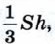Следовательно, площадь сечения конуса равна площади сечения пирамиды. Поэтому и его объём равен объёму пирамиды, т. е. равен что и требовалось доказать.

Продолжение >>>