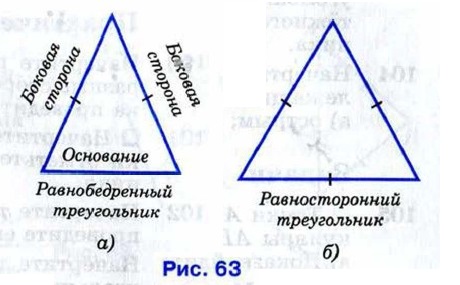
Свойства равнобедренного треугольника

Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника (рис. 63, а).

Треугольник, все стороны которого равны, называется равносторонним (рис. 63, б).

равносторонний треугольник

Докажем две теоремы о свойствах равнобедренного треугольника.

Теорема

В равнобедренном треугольнике углы при основании равны.

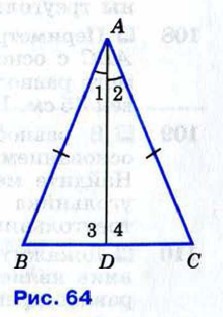
Доказательство

Рассмотрим равнобедренный треугольник АВС с основанием ВС и докажем, что ∠B = ∠C. Пусть AD — биссектриса треугольника АВС (рис. 64). Треугольники ABD и ACD равны по первому признаку равенства треугольников (АВ = АС по условию, AD — общая сторона, ∠1 = ∠2, так как AD — биссектриса). В равных треугольниках против равных сторон лежат равные углы, поэтому ∠B = ∠C. Теорема доказана.

равнобедренный треугольник

Теорема

В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

Доказательство

Обратимся снова к рисунку 64, на котором АВС — равнобедренный треугольник с основанием ВС, AD — его биссектриса.

Из равенства треугольников ABD и ACD следует, что BD = DC и ∠3 = ∠4. Равенство BD = DC означает, что точка D — середина стороны ВС, и поэтому AD — медиана треугольника АВС. Так как углы 3 и 4 — смежные и равны друг другу, то они прямые. Следовательно, отрезок AD является также высотой треугольника АВС. Теорема доказана.

Мы установили, что биссектриса, медиана и высота равнобедренного треугольника, проведённые к основанию, совпадают. Поэтому справедливы также утверждения:

1. Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой.
2. Медиана равнобедренного треугольника, проведённая к основанию, является высотой и биссектрисой.