|
|
|
|
|
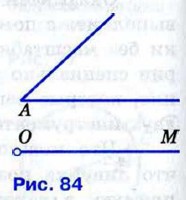
§ 4. Задачи на построение Примеры задач на построениеПостроение угла, равного данномуЗадача Отложить от данного луча угол, равный данному. Решение Данный угол с вершиной А и луч ОМ изображены на рисунке 84. Требуется построить угол, равный углу А, так, чтобы одна из его сторон совпала с лучом ОМ.
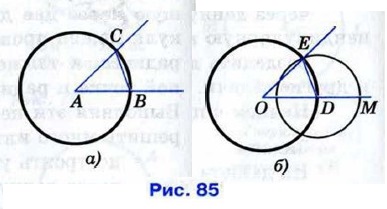
Проведём окружность произвольного радиуса с центром в вершине А данного угла. Эта окружность пересекает стороны угла в точках В и С (рис. 85, а). Затем проведём окружность того же радиуса с центром в начете данного луча ОМ. Она пересекает луч в точке D (рис. 85, б). После этого построим окружность с центром D, радиус которой равен ВС. Окружности с центрами О и D пересекаются в двух точках. Одну из этих точек обозначим буквой Е. Докажем, что угол МОЕ — искомый.
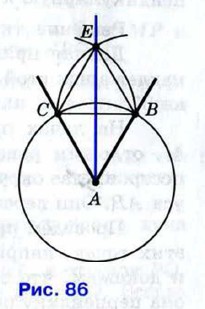
Рассмотрим треугольники АВС и ODE. Отрезки АВ и АС являются радиусами окружности с центром А, а отрезки OD и ОЕ — радиусами окружности с центром О (см. рис. 85, б). Так как по построению эти окружности имеют равные радиусы, то AB = OD, АС = ОЕ. Также по построению ВС = DE. Следовательно, То же построение можно выполнить и на местности, если вместо циркуля воспользоваться верёвкой. Построение биссектрисы углаЗадача Построить биссектрису данного угла. Решение Данный угол ВАС изображён на рисунке 86. Проведём окружность произвольного радиуса с центром в вершине А. Она пересечёт стороны угла в точках В и С.
Затем проведём две окружности одинакового радиуса ВС с центрами в точках В и С (на рисунке изображены лишь части этих окружностей). Они пересекутся в двух точках, из которых хотя бы одна лежит внутри угла. Обозначим её буквой Е. Докажем, что луч АЕ является биссектрисой данного угла ВАС. Рассмотрим треугольники АСЕ и АВЕ. Они равны по трём сторонам. В самом деле, АЕ — общая сторона; АС и АВ равны как радиусы одной и той же окружности; СЕ = BE по построению. Из равенства треугольников АСЕ и АВЕ следует, что ∠CAE = ∠BAE, т. е. луч АЕ — биссектриса данного угла ВАС.
|
|
|



 АВС =
АВС =