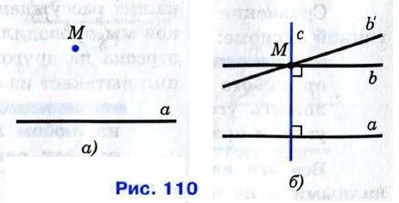
Аксиома параллельных прямых

Рассмотрим произвольную прямую а и точку М, не лежащую на ней (рис. 110, а). Докажем, что через точку М можно провести прямую, параллельную прямой а. Для этого проведём через точку М две прямые: сначала прямую с перпендикулярно к прямой а, а затем прямую b перпендикулярно к прямой с (рис. 110, (б). Так как прямые а и b перпендикулярны к прямой с, то они параллельны.

Итак, через точку М проходит прямая b, параллельная прямой а. Возникает следующий вопрос: можно ли через точку М провести ещё одну прямую, параллельную прямой а?

Нам представляется, что если прямую b «повернуть» даже на очень малый угол вокруг точки М, то она пересечёт прямую а (прямая b' на рисунке 110,6). Иными словами, нам кажется, что через точку М нельзя провести другую прямую (отличную от b), параллельную прямой а. А можно ли это утверждение доказать?

Этот вопрос имеет большую историю. В «Началах» Евклида содержится постулат (пятый постулат Евклида), из которого следует, что через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной. Многие математики, начиная с древних времён, предпринимали попытки доказать пятый постулат Евклида, т. е. вывести его из других аксиом. Однако эти попытки каждый раз оказывались неудачными. И лишь в прошлом веке было окончательно выяснено, что утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, не может быть доказано на основе остальных аксиом Евклида, а само является аксиомой.

Огромную роль в решении этого непростого вопроса сыграл великий русский математик Николай Иванович Лобачевский (1792—1856).

Лобачевский

Окончание >>>