Теоремы об углах, образованных двумя параллельными прямыми и секущей

Во всякой теореме различают две части: условие и заключение. Условие теоремы — это то, что дано, а заключение — то, что требуется доказать.

Рассмотрим, например, теорему, выражающую признак параллельности двух прямых: если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

В этой теореме условием является первая часть утверждения: «при пересечении двух прямых секущей накрест лежащие углы равны» (это дано), а заключением — вторая часть: «прямые параллельны» (это требуется доказать).

Теоремой, обратной данной, называется такая теорема, в которой условием является заключение данной теоремы, а заключением — условие данной теоремы. Докажем теоремы, обратные трём теоремам п. 25.

Теорема

Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

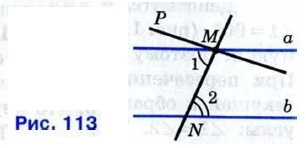
Доказательство

Пусть параллельные прямые а и b пересечены секущей MN. Докажем, что накрест лежащие углы, например 1 и 2, равны (рис. 113).

рис. 113

Допустим, что углы 1 и 2 не равны. Отложим от луча MN угол PMN, равный углу 2, так, чтобы ∠PMN и ∠2 были накрест лежащими углами при пересечении прямых МР и b секущей MN. По построению эти накрест лежащие углы равны, поэтому МР || b. Мы получили, что через точку М проходят две прямые (прямые а и МР), параллельные прямой Ь. Но это противоречит аксиоме параллельных прямых. Значит, наше допущение неверно и ∠1 = ∠2. Теорема доказана.

Замечание

При доказательстве этой теоремы мы использовали способ рассуждений, который называется методом доказательства от противного.

Мы предположили, что при пересечении параллельных прямых а и b секущей MN накрест лежащие углы 1 и 2 не равны, т. е. предположили противоположное тому, что нужно доказать. Исходя из этого предположения, путём рассуждений мы пришли к противоречию с аксиомой параллельных прямых. Это означает, что наше предположение неверно и, следовательно, ∠1 = ∠2.

Такой способ рассуждений часто используется в математике. Мы им пользовались и ранее, например в п. 12 при доказательстве того, что две прямые, перпендикулярные к третьей, не пересекаются. Этим же методом мы пользовались в п. 28 при доказательстве следствий 1⁰ и 2⁰ из аксиомы параллельных прямых.

Окончание >>>