Задачи к § 2. Аксиома параллельных прямых (окончание)

209. На рисунке 120 а || b, с || d, ∠4 = 45°. Найдите углы 1, 2 и 3.

рисунок 120

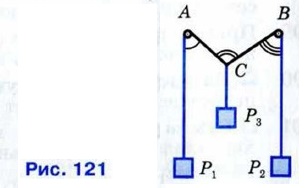
210. Два тела Р₁ и Р₂ подвешены на концах нити, перекинутой через блоки А и В (рис. 121). Третье тело Р₃ подвешено к той же нити в точке С и уравновешивает тела Р₁ и Р₂. (При этом АР₁ || ВР₂ || СР₃.) Докажите, что ∠ACB = ∠CAP₁ + ∠CBP₂.

рисунок 121

211. Две параллельные прямые пересечены секущей. Докажите, что: а) биссектрисы накрест лежащих углов параллельны; б) биссектрисы односторонних углов перпендикулярны.

212. Прямые, содержащие высоты АА₁ и ВВ₁ треугольника АВС, пересекаются в точке Н, угол В — тупой, ∠C = 20°. Найдите угол АHВ.

Ответы к задачам § 2. Аксиома параллельных прямых

196. Одну прямую.

197. Три или четыре.

198. Да.

201. 105°, 105°.

202. а || с.

203. б) Четыре угла по 55°, четыре других угла по 125°.

205. 92°.

206. а) Да; б) да.

207. а) Нет; б) да.

208. 115° и 65°.

209. ∠1 = 135°, ∠2 = 45°, ∠3=135°.

210. Указание. Рассмотреть продолжение луча СР₃.

<<< К началу