|
|
|
|
|
§ 2. Соотношения между сторонами и углами треугольника Неравенство треугольникаТеорема
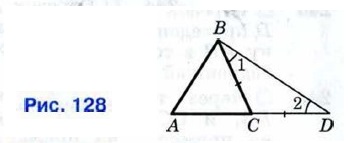
Доказательство Рассмотрим произвольный треугольник АВС и докажем, что АВ < АС + СВ. Отложим на продолжении стороны АС отрезок CD, равный стороне СВ (рис. 128). В равнобедренном треугольнике BCD ∠1 = ∠2, а в треугольнике ABD ∠ABD> ∠1 и, значит, ∠ABD > ∠2.
Так как в треугольнике против большего угла лежит большая сторона, то АВ < AD. Но AD = АС + CD = АС + СВ, поэтому АВ < АС + СВ. Теорема доказана. Следствие
Каждое из этих неравенств называется неравенством треугольника.
|
|
|