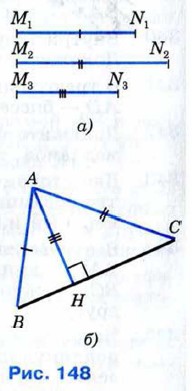
Задачи повышенной трудности к главам: Глава III. Параллельные прямые и Глава IV. Соотношения между сторонами и углами треугольника (продолжение)

351. Постройте треугольник по двум сторонам и высоте к третьей стороне.

Решение

Даны три отрезка M₁N₁, MN₂, M₃N₃ (рис. 148, а). Требуется, построить такой треугольник АВС, у которого две стороны, скажем АВ и АС, равны соответственно данным отрезкам M₁N₁ и M₂N₂, а высота АН равна отрезку M₃N₃. Проведём решение задачи по описанной схеме.

рис. 148

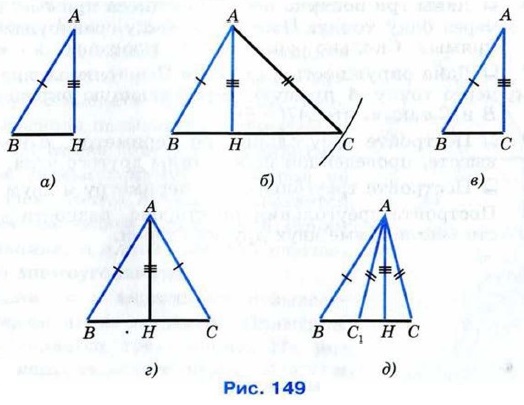
Анализ

Допустим, что искомый треугольник АВС построен (рис. 148, б). Мы видим, что сторона АВ и высота АН являются гипотенузой и катетом прямоугольного треугольника АВН. Поэтому построение треугольника АВС можно провести по такому плану: сначала построить прямоугольный треугольник АВН, а затем достроить его до всего треугольника АВС.

Построение

Строим прямоугольный треугольник АВН, у которого гипотенуза АВ равна отрезку M₁N₁, а катет АН равен данному отрезку M₃N₃. Как это сделать, мы знаем (задача 314, в). На рисунке 149, а изображён построенный треугольник АВН. Затем проводим окружность радиуса M₂N₂ с центром в точке А. Одну из точек пересечения этой окружности с прямой ВН обозначим буквой С. Проведя отрезки ВС и АС, получим искомый треугольник АВС (рис. 149, б).

рис. 149

Доказательство

Треугольник АВС действительно искомый, так как по построению сторона АВ равна M₁N₁, сторона АС равна M₂N₂, а высота АН равна M₃N₃, т. е. треугольник АВС удовлетворяет всем условиям задачи.

Исследование

Нетрудно сообразить, что задача имеет решение не при любых данных отрезках M₁N₁, M₂N₂, M₃N₃. В самом деле, если хотя бы один из отрезков M₁N₁ и M₂N₂ меньше M₃N₃, то задача не имеет решения, так как наклонные АВ и АС не могут быть меньше перпендикуляра АН. Задача не имеет решения и в том случае, когда M₁N₁ = M₂N₂ = M₃N₃ (объясните почему). В остальных случаях задача имеет решение. Если M₁N₁ > M₃N₃, a M₂N₂ = M₃N₃, то задача имеет единственное решение: в этом случае сторона АС совпадает с высотой АН и искомый треугольник является прямоугольным (рис. 149, в). Если M₁N₁ > M₃N₃, a M₂N₂ = M₁N₁, то задача также имеет единственное решение: в этом случае треугольник АВС равнобедренный (рис. 149, г). И наконец, если M₁N₁ > M₃N₃, M₂N₂ > M₃N₃ и M₁N₁ ≠ M₂N₂ то задача имеет два решения — треугольники АВС и АВС, на рисунке 149, д.

352. Даны две точки А и В и прямая а, не проходящая через эти точки. На прямой а постройте точку, равноудалённую от точек А и В. Всегда ли задача имеет решение?

353. Постройте точку, лежащую на данной окружности и равноудалённую от концов данного отрезка. Сколько решений может иметь задача?

354. Через три данные точки проведите окружность. Всегда ли задача имеет решение?

355. Точки А и В лежат по одну сторону от прямой а. Постройте точку М прямой а так, чтобы сумма AM + МВ имела наименьшее значение, т. е. была бы меньше суммы АХ + ХВ, где X — любая точка прямой а, отличная от М.

356. Постройте прямоугольный треугольник АВС, если даны острый угол В и биссектриса BD.

357. На данной окружности постройте точку, равноудалённую от двух данных пересекающихся прямых. Сколько решений может иметь задача?

358. Даны три попарно пересекающиеся прямые, не проходящие через одну точку. Постройте точку, равноудалённую от этих прямых. Сколько решений имеет задача?

359. Дана окружность с центром О и точка А вне её. Проведите через точку А прямую, пересекающую окружность в точках В и С таких, что АВ = ВС.

360. Постройте треугольник по периметру, одному из углов и высоте, проведённой из вершины другого угла.

361. Постройте треугольник по периметру и двум углам.

362. Постройте треугольник по стороне, разности углов при этой стороне и сумме двух других сторон.

<<< К началу Ответы >>>