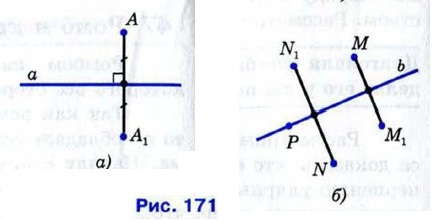
Осевая и центральная симметрии

Две точки А и A₁ называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА₁ и перпендикулярна к нему (рис. 171, а). Каждая точка прямой а считается симметричной самой себе. На рисунке 171, б точки М и М₁, N и N₁ симметричны относительно прямой b, а точка Р симметрична самой себе относительно этой прямой.

рис. 171

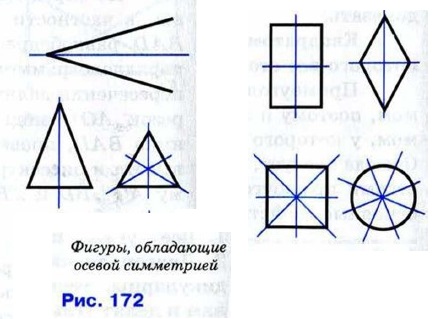
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией.

Приведём примеры фигур, обладающих осевой симметрией (рис. 172). У неразвёрнутого угла одна ось симметрии — прямая, на которой расположена биссектриса угла. Равнобедренный (но не равносторонний) треугольник имеет также одну ось симметрии, а равносторонний треугольник — три оси симметрии. Прямоугольник и ромб, не являющиеся квадратами, имеют по две оси симметрии, а квадрат — четыре оси симметрии. У окружности их бесконечно много — любая прямая, проходящая через её центр, является осью симметрии.

рис. 172

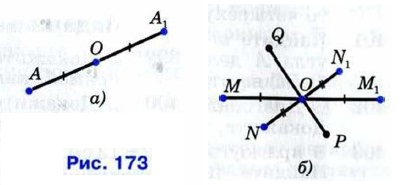
Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника и ромба, разносторонний треугольник.

Две точки А и A₁ называются симметричными относительно точки О, если О — середина отрезка АА₁ (рис. 173, а). Точка О считается симметричной самой себе. На рисунке 173, б точки М и М₁, N и N₁ симметричны относительно точки О, а точки Р и Q не симметричны относительно этой точки.

рис. 173

Окончание >>>