Понятие площади многоугольника (окончание)

Вывод этих формул основан на свойствах площадей, которые мы сейчас рассмотрим.

Прежде всего отметим, что если два многоугольника равны, то единица измерения площадей и её части укладываются в таких многоугольниках одинаковое число раз, т. е. имеет место следующее свойство:

1⁰. Равные многоугольники имеют равные площади.

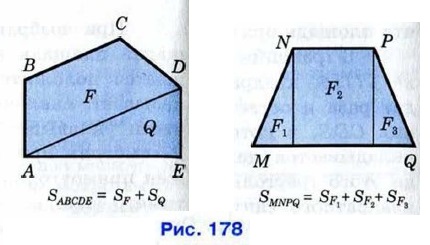
Далее, пусть многоугольник составлен из нескольких многоугольников так, что внутренние области любых двух из этих многоугольников не имеют общих точек, как показано на рисунке 178. Очевидно, величина части плоскости, занимаемой всем многоугольником, является суммой величин тех частей плоскости, которые занимают составляющие его многоугольники. Итак:

рис. 178

2⁰. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

Свойства 1⁰ и 2⁰ называют основными свойствами площадей. Напомним, что аналогичными свойствами обладают длины отрезков.

Наряду с этими свойствами нам понадобится ещё одно свойство площадей.

3⁰. Площадь квадрата равна квадрату его стороны.

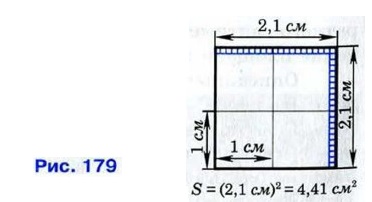
Краткую формулировку этого свойства следует понимать так: если сторона квадрата при выбранной единице измерения отрезков выражается числом а, то площадь этого квадрата выражается числом а².

На рисунке 179 изображён квадрат, сторона которого равна 2,1 см. Он состоит из четырёх квадратных сантиметров и сорока одного квадратного миллиметра. Таким образом, площадь квадрата равна 4,41 см², что равно квадрату его стороны: 4,41 = (2,1)². Доказательство утверждения 3⁰ приведено в следующем пункте.

рис. 179

Если площади двух многоугольников равны, то эти многоугольники называются равновеликими. Если один многоугольник разрезан на несколько многоугольников и из них составлен другой многоугольник, то такие многоугольники называются равносоставленными. Например, прямоугольник со сторонами, равными 2 см и Зсм (см. рис. 177, а), равносоставлен с прямоугольником со сторонами, равными 1 см и 6 см. Ясно, что любые два равносоставленных многоугольника равновеликие (см. основные свойства площадей). Оказывается, что верно и обратное утверждение: если два многоугольника равновеликие, то они равносоставленные. Это утверждение называется теоремой Бойяи — Гервина. Венгерский математик Ф. Бойяи доказал эту теорему в 1832 г., а немецкий математик-любитель П. Гервин независимо от Ф. Бойяи доказал её в 1833 г.

<<< К началу