|
|
|
|
Главная >> Машиностроительное черчение. Инженерная графика. Чекмарев |
|
|
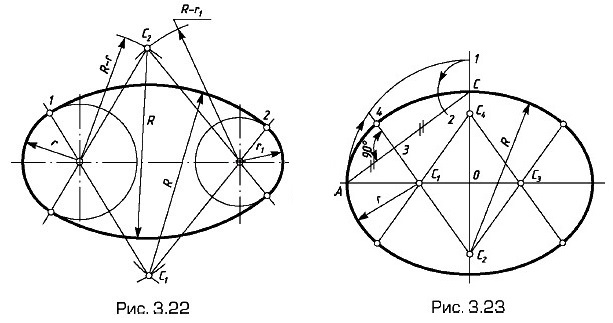
Кривые линии и их применение в чертежах СопряженияПостроение оваловОвал — это фигура, состоящая из двух опорных окружностей, внутренне сопряженных дугами. Построение овала с опорными окружностями разных диаметров (рис. 3.22) сводится к построению выпуклого сопряжения двух дуг (см. рис. 3.23) двумя дугами одинакового радиуса из центров С1 и С2. Такой овал имеет одну ось симметрии. Если опорные окружности одинакового диаметра, то овал имеет две оси симметрии.
Построение овала по двум заданным осям (рис. 3.23). Широко применяется, например, следующее построение. На продолжении малой оси отмечают точку 1([ОА] = [О — 1]) и на отрезке АС дугой радиуса С — 1 отмечают точку 2. Через середину 3 отрезка А — 2 проводят перпендикуляр и находят центры С1 опорной окружности радиуса r и С2 сопрягающей дуги R. Точка сопряжения (4) = (circ1 r) 1 circ — условная запись слов «окружность» или «дуга окружности». Построение сопряженийКасательная из точки (А) к окружности (рис. 3.24). На отрезке ОА как на диаметре строят окружность радиуса R = 0,5[ОA]. Точка 1 ее пересечения с заданной окружностью радиуса r — точка сопряжения (О —
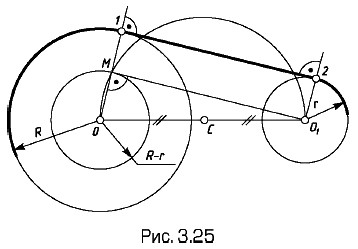
Касательная к двум дугам (R и r, рис. 3.25, внешнее касание). Проводят дугу радиуса R - r из центра О дуги большего радиуса. Строят касательную MO1 к этой дуге, проходящую через центр дуги меньшего радиуса (
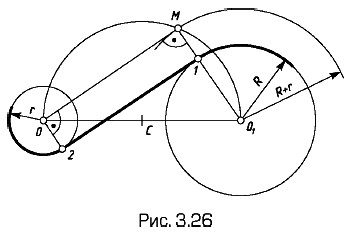
Касательные к двум дугам (R и r, рис. 3.26, внутреннее касание). Из центра О3 дуги большего радиуса проводят дугу радиуса R + r. Строят касательную к этой дуге в точке М, проходящую через центр О (см. рис. 3.24). Отмечают точку касания 1 на дуге радиуса R, строят точку касания 2 на дуге радиуса R (О — 2 ⊥ ОМ) или О — 2 || О1М. Проводят искомую касательную.
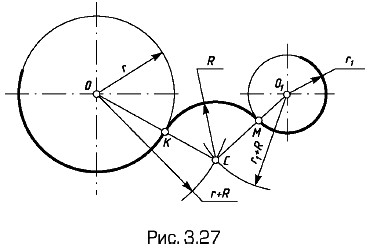
Сопряжение двух дуг вогнутое (рис. 3.27). Радиус сопряжения R; центр (С) = (circ (r + R)) Точки сопряжения (1) = (circ r)
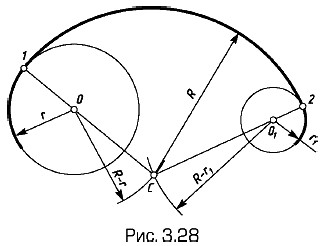
Сопряжение двух дуг выпуклое (рис. 3.28). Радиус сопряжения R; центр (C) = (circ (R - r)) Точки сопряжения (1) = (circ r)
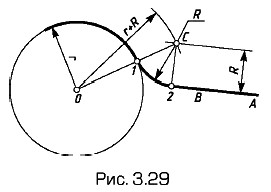
Сопряжение окружности с прямой (рис. 3.29. Центр С дуги сопряжения радиуса R строят в пересечении дуги радиуса (r + R) и прямой, параллельной заданной прямой АВ на расстоянии [R]. Точки 1 и 2 — точки сопряжения.
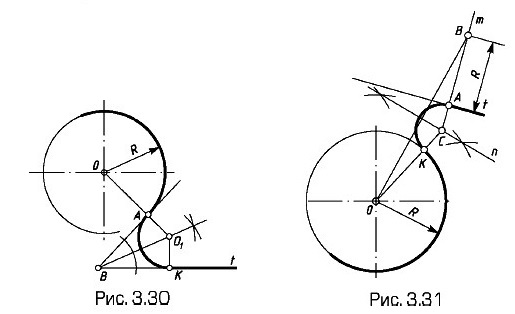
Задана точка сопряжения А на окружности (рис. 3.30 — внешнее касание). Центр дуги сопряжения — точка пересечения луча ОА, проведенного через точку сопряжения А и центр заданной окружности, и биссектрисы угла ABK, образованного касательной АВ в точке сопряжения и заданной прямой t. Радиус сопрягающей дуги равен расстоянию O1A; O1K⊥t, где K — точка сопряжения на прямой t.
Задана на прямой t точка сопряжения А (рис. 3.31 — внешнее касание). В данной точке А на прямой восстанавливают перпендикуляр m и откладывают на нем отрезок АВ, равный радиусу R заданной окружности. Полученную точку В соединяют с центром О окружности и из середины отрезка OB восстанавливают к нему перпендикуляр n. В точке пересечения перпендикуляров m и n отмечают точку C — центр искомой дуги сопряжения. Точка K — точка сопряжения; CK — радиус дуги сопряжения.
|
|
|



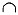 (C1C2). Центры С3 и С4 находят как симметричные. Заметим, что по двум осям может быть построено бесконечно большое число овалов.
(C1C2). Центры С3 и С4 находят как симметричные. Заметим, что по двум осям может быть построено бесконечно большое число овалов.
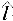 — А = 90°). Через точки А и 1 проводят искомую касательную.
— А = 90°). Через точки А и 1 проводят искомую касательную.
 1 = 90°). На продолжении луча ОМ отмечают точку касания 1. Из центра О1 проводят прямую (О1 - 2) || (О - 1), через точки 1 и 2 — искомую касательную.
1 = 90°). На продолжении луча ОМ отмечают точку касания 1. Из центра О1 проводят прямую (О1 - 2) || (О - 1), через точки 1 и 2 — искомую касательную.