Главная >> Машиностроительное черчение. Инженерная графика. Чекмарев

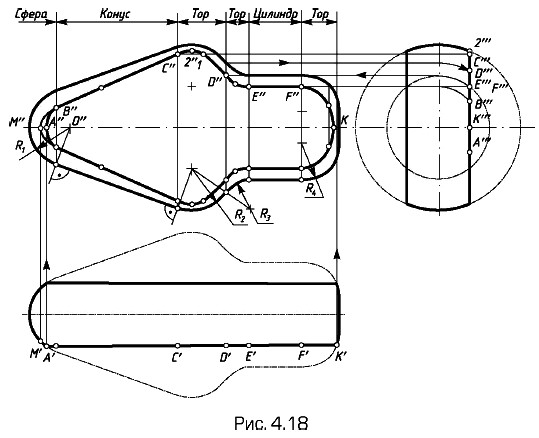
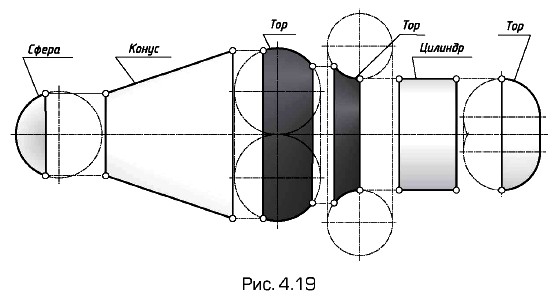
Элементы геометрии деталей

Построение линии среза на поверхности тела вращения сложной формы

Многие детали приборов и машин имеют в своей основе форму тела вращения со сложной формой поверхности. Такое тело можно рассматривать как состоящее из частей элементарных тел вращения — цилиндра, конуса, сферы и тора, или кругового кольца. Детали из такого тела вращения часто конструируют путем среза части тела плоскостью, параллельной оси. При этом в пересечении поверхности тела с плоскостью среза образуются сложные линии, построение которых и рассмотрено ниже. Эти линии, являющиеся частным случаем линии пересечения поверхности вращения с плоскостью (плоскость параллельна оси), называются линиями среза.

Пример чертежа такого тела с построенными линиями среза приведен на рис. 4.18. На чертеже оставлены некоторые вспомогательные линии построений и точки. При выполнении построений прежде всего устанавливают границы заданных поверхностей вращения и определяют элементарные поверхности — цилиндр, конус, сфера, тор. Для этого достаточно мысленно или на черновике дополнить участки поверхностей, как показано на рис. 4.19. На рисунке все поверхности для наглядности раздвинуты вдоль оси вращения.

Разграничение участков элементарных поверхностей позволяет определить характер отдельных участков линий среза и правильно выбрать количество и расположение вспомогательных секущих плоскостей, необходимых для построения промежуточных точек на линии среза.

На чертеже границами поверхностей вращения являются линии касания или пересечения элементарных поверхностей. Их проекции в виде отрезков прямых, перпендикулярных оси вращения, проводят через проекции точек сопряжения или пересечения образующих. Так, на рис. 4.18 граница между сферой и конусом проведена через точку сопряжения дуги радиусом R₁ и образующей конуса. Эта точка определена с помощью перпендикуляра из проекции O" центра сферы к образующей конуса. Граница между конусом и тором с радиусом образующей R₂ проведена через точку касания образующей конуса и дуги радиуса R₂. Точка сопряжения определена с помощью перпендикуляра, проведенного из центра дуги радиуса R₂ к образующей конуса. Граница между тором с радиусом образующей R₂ и тором с радиусом образующей R3 проведена через точку сопряжения дуг радиуса R₂ и R₃. Точка сопряжения найдена с помощью прямой, соединяющей центры дуг. Границы между тором с радиусом образующей R₃ и цилиндром, между этим же цилиндром и тором с радиусом образующей R₄ проведены через точки сопряжения дуг указанных радиусов с образующей цилиндра. Они проходят и через центры дуг.

Построенные границы элементарных поверхностей можно рассматривать и как линии пересечения поверхности вращения плоскостями, перпендикулярными оси, в данном случае — профильными плоскостями. Профильные проекции этих линий — окружности. В пересечении их с профильными проекциями плоскостей среза отмечают профильные проекции характерных точек на линии среза. Пример построения профильной проекции D"' и по ней фронтальной проекции D" отмечен на рис. 4.18. По положению проекций B"', C"', E"', F"' строят фронтальные проекции B", C", E", F" точек линии среза. Проекции A", K" (их проекции A"', K"' совпадают) построены по горизонтальным проекциям A', K'.

В данном примере линия среза и ее фронтальная проекция состоят из следующих участков: на сфере радиуса R₁ — дуги окружности радиуса A"O"; на конусе — части гиперболы с вершиной M"; на торе с радиусом образующей R₂ — части кривой Персея; на торе с радиусом образующей R₃ — части кривой Персея; на цилиндре — отрезки прямых, параллельных оси; на торе с радиусом образующей R₄ — части кривой Персея. Зная вид линии среза и положение проекций характерных и крайних точек линий, можно ограничиться построением проекций минимального количества промежуточных точек. В данном примере на рис. 4.18 показано построение проекций «промежуточной» точки на участке K"F", а также построенные проекции «промежуточных» точек на участках B"С", C"D", D"E". Следует отметить, что точка 1" симметрична точке C", а точка 2" — наиболее удаленная от оси.

Следующий параграф >>>